(本小题满分12分)已知函数 ,
, ,函数
,函数
在 、
、 处取得极值,其中
处取得极值,其中 。
。
(Ⅰ)求实数 的取值范围;
的取值范围;
(Ⅱ)判断 在
在 上的单调性;
上的单调性;
(Ⅲ)已知 在
在 上的最大值比最小值大
上的最大值比最小值大  ,若方程
,若方程 有3个不同的解,
有3个不同的解,
求实数 的取值范围。
的取值范围。
(本小题满分8分)已知函数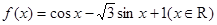 .
.
(Ⅰ)求函数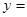
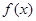 的最大值,并指出取得最大值时相应的
的最大值,并指出取得最大值时相应的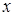 的值;
的值;
(Ⅱ)求函数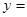
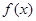 的单调增区间.
的单调增区间.
已知数列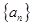 :
: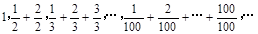
①观察规律,归纳并计算数列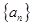 的通项公式,它是个什么数列?
的通项公式,它是个什么数列?
②若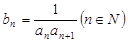 ,设
,设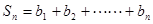 ,求
,求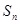
③设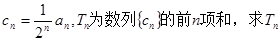
某研究所计划利用“神七”宇宙飞船进行新产品搭载实验,计划搭载新产品A、B,要根据该产品的研制成本、产品重量、搭载实验费用和预计产生收益来决定具体安排,通过调查,有关数据如表:
| 产品A(件) |
产品B(件) |
||
| 研制成本与塔载 费用之和(万元/件) |
20 |
30 |
计划最大资 金额300万元 |
| 产品重量(千克/件) |
10 |
5 |
最大搭载 重量110千克 |
| 预计收益(万元/件) |
80 |
60 |
试问:如何安排这两种产品的件数进行搭载,才能使总预计收益达到最大,最大收益是多少?
已知函数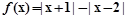
(1)把上式写成分段函数,并画出其图像.
(2)求不等式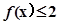 的解集.
的解集.
(3)若存在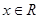 使不等式
使不等式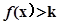 ,试求实数k的取值范围.
,试求实数k的取值范围.
数列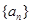 中,
中,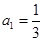 ,前
,前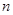 项和
项和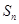 满足
满足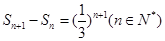 。
。
(Ⅰ)求数列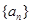 的通项公式,以及前
的通项公式,以及前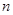 项和
项和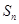 ;
;
(Ⅱ)若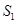 ,
,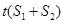 ,
,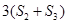 成等差数列,求实数
成等差数列,求实数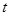 的值。
的值。