(本小题满分12分)设 为数列
为数列 的前
的前 项和,
项和,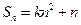 ,
, ,其中
,其中 是常数.
是常数.
(1)求 及
及 ;
;
(2)若对于任意的 ,
, ,
, ,
,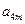 成等比数列,求
成等比数列,求 的值.
的值.
现有甲、乙两个靶.某射手向甲靶射击两次,每次命中的概率为 ,每命中一次得1分,没有命中得0分;向乙靶射击一次,命中的概率为
,每命中一次得1分,没有命中得0分;向乙靶射击一次,命中的概率为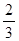 ,命中得2分,没有命中得0分.该射手每次射击的结果相互独立.假设该射手完成以上三次射击.
,命中得2分,没有命中得0分.该射手每次射击的结果相互独立.假设该射手完成以上三次射击.
(I)求该射手恰好命中两次的概率;
(II)求该射手的总得分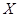 的分布列及数学期望
的分布列及数学期望 ;
;
已知数列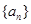 满足
满足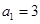 ,
, ,数列
,数列 满足
满足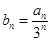 .
.
(1)证明数列 是等差数列并求数列
是等差数列并求数列 的通项公式;
的通项公式;
(2)求数列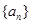 的前n项和
的前n项和 .
.
已知函数 是定义在
是定义在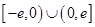 上的奇函数,当
上的奇函数,当 时,
时, 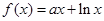 (其中e是自然界对数的底,
(其中e是自然界对数的底,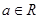 )
)
(Ⅰ)设 ,求证:当
,求证:当 时,
时, ;
;
(Ⅱ)是否存在实数a,使得当 时,
时, 的最小值是3 ?如果存在,求出实数a的值;如果不存在,请说明理由。
的最小值是3 ?如果存在,求出实数a的值;如果不存在,请说明理由。
已知函数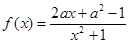 ,其中
,其中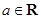 .
.
(1)若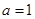 时,记
时,记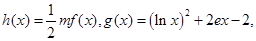 存在
存在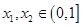 使
使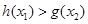 成立,求实数
成立,求实数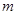 的取值范围;
的取值范围;
(2)若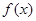 在
在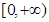 上存在最大值和最小值,求
上存在最大值和最小值,求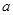 的取值范围.
的取值范围.
已知函数
(1)当a=1时,求曲线在点(3, )处的切线方程
)处的切线方程
(2)求函数 的单调递增区间
的单调递增区间