(本小题满分10分)
已知函数 ,在
,在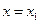 和
和 处取得极值.
处取得极值.
(I)若 ,且
,且 ,求
,求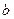 的最大值;
的最大值;
(II)设 ,若
,若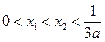 ,且
,且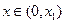 ,证明:
,证明: .
.
设函数 .
.
(1)求函数 的最小正周期和单调递增区间;
的最小正周期和单调递增区间;
(2)当 时,
时, 的最大值为2,求
的最大值为2,求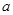 的值,并求出
的值,并求出 的对称轴方程.
的对称轴方程.
已知函数 ∈R).
∈R).
(1)若 ,求
,求 点(
点( )处的切线方程;
)处的切线方程;
(2)设a≤0,求 的单调区间;
的单调区间;
(3)设a<0,且对任意的 ,
, ≤
≤ ,试比较
,试比较 与
与 的大小.
的大小.
已知函数 (e为自然对数的底数),a>0.
(e为自然对数的底数),a>0.
(1)若函数 恰有一个零点,证明:
恰有一个零点,证明: ;
;
(2)若 ≥0对任意x∈R恒成立,求实数a的取值集合.
≥0对任意x∈R恒成立,求实数a的取值集合.
记公差不为0的等差数列 的前
的前 项和为
项和为 ,S3=9,
,S3=9, 成等比数列.
成等比数列.
(1)求数列 的通项公式
的通项公式 及
及 ;
;
(2)若 , n=1,2,3, ,问是否存在实数
, n=1,2,3, ,问是否存在实数 ,使得数列
,使得数列 为单调递增数列?若存在,请求出
为单调递增数列?若存在,请求出 的取值范围;不存在,请说明理由.
的取值范围;不存在,请说明理由.
在△ABC中,a,b,c分别是内角A,B,C的对边, .
.
(1)若 ,求△ABC的面积S△ABC;
,求△ABC的面积S△ABC;
(2)若 是边
是边 中点,且
中点,且 ,求边
,求边 的长.
的长.