（本小题满分12分）（注意：在试题卷上作答无效）为赢得2010年上海世博会的制高点，某公司最近进行了世博特许产品的市场分析，调查显示，该产品每件成本9元，售价为30元，每天能卖出432件，该公司可以根据情况可变化价格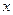
（
）元出售产品；若降低价格，则销售量增加，且每天多卖出的产品件数与商品单价的降低值
的平方成正比，已知商品单价降低2元时，每天多卖出24件；若提高价格，则销售减少，减少的件数与提高价格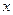成正比，每提价1元则每天少卖8件，且仅在提价销售时每件产品被世博管委会加收1元的管理费。
（Ⅰ）试将每天的销售利润
表示为价格变化值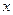的函数；
（Ⅱ）试问如何定价才能使产品销售利润最大？
（本小题满分14分）
已知函数
（1）求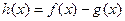
的单调区间；
（2）求证：当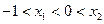
时，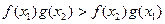
；
（3）求证：
（本小题满分12分）
已知函数
（1）若
求
的单调区间及的最小值；
（2）求的单调区间；
（3）试比较
的大小，
，并证明你的结论。
（本小题满分12）
设二次函数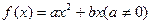
满足条件：
①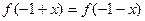
；②函数
的图象与直线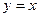
只有一个公共点。
（1）求的解析式；
（2）若不等式
时恒成立，求实数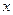
的取值范围。
（本小题满分12分）
为保增长、促发展，某地计划投资甲、乙两项目，市场调研得知，甲项目每投资百万元需要配套电能2万千瓦，可提供就业岗位24个，增加GDP260万元；乙项目每项投资百万元需要配套电能4万千瓦，可提供就业岗位32个，增加GDP200万元，已知该地为甲、乙两项目最多可投资3000万元，配套电能100万千瓦，并要求它们提供的就业岗位不少于800个，如何安排甲、乙两项目的投资额，增加的GDP最大？
（本小题满分12分）
设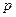
：函数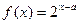
在区间（4，+∞）上单调递增；
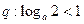，如果“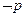
”是真命题，“
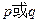”也是真命题，求实数
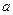的取值范围。