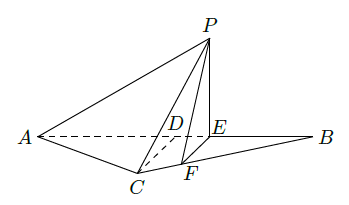
如图所示,等腰三角形
的底边
,高
.点
是线段
上异于
的动点.点
在
边上,且
.现沿
将
折起到
的位置,使
.
记
表示四棱锥
的体积。
(1)求
的表达式;
(2)当
为何值时,
取得最大值?
(3)当
取得最大值时,求异面直线
与
所成角的余弦值。
通过随机询问110名不同的大学生是否爱好某项运动,得到如下的列联表:
| 男 |
女 |
总计 |
|
| 爱好 |
40 |
20 |
60 |
| 不爱好 |
20 |
30 |
50 |
| 总计 |
60 |
50 |
110 |
附:
 |
0.050 |
0.010 |
0.001 |
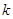 |
3.841 |
6.635 |
10.828 |
试考查大学生“爱好该项运动是否与性别有关”,若有关,请说明有多少把握。
已知函数 在区间
在区间 ,
, 上有极大值
上有极大值 .
.
(1)求实常数m的值.
(2)求函数 在区间
在区间 ,
, 上的极小值.
上的极小值.
已知函数
(1)若 ,试确定函数
,试确定函数 的单调区间;
的单调区间;
(2)若 ,且对于任意
,且对于任意 ,
, 恒成立,试确定实数
恒成立,试确定实数 的取值范围;
的取值范围;
设 ,
, .
.
(1)令 ,讨论
,讨论 在
在 内的单调性并求极值;
内的单调性并求极值;
(2)求证:当 时,恒有
时,恒有 .
.
已知函数
 ,函数
,函数
⑴当 时,求函数
时,求函数 的表达式;
的表达式;
⑵若 ,函数
,函数 在
在 上的最小值是2 ,求
上的最小值是2 ,求 的值;
的值;