通过随机询问110名不同的大学生是否爱好某项运动,得到如下的列联表:
| |
男 |
女 |
总计 |
| 爱好 |
40 |
20 |
60 |
| 不爱好 |
20 |
30 |
50 |
| 总计 |
60 |
50 |
110 |
附: 
 |
0.050 |
0.010 |
0.001 |
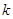 |
3.841 |
6.635 |
10.828 |
试考查大学生“爱好该项运动是否与性别有关”,若有关,请说明有多少把握。
已知数列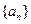 的前
的前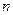 项和为
项和为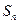 ,且
,且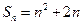 .数列
.数列 中,
中, ,
,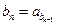
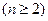 .(1)求数列
.(1)求数列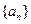 的通项公式;(2)若存在常数
的通项公式;(2)若存在常数 使数列
使数列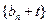 是等比数列,求数列
是等比数列,求数列 的通项公式;(3)求证:①
的通项公式;(3)求证:①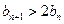 ;②
;②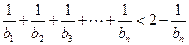 .
.
已知定义在R上的函数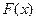 满足
满足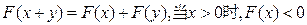 ,且对任意的
,且对任意的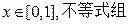
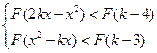 均成立,(1)求证:函数
均成立,(1)求证:函数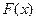 在R上为减函数(2)求实数k的取值范围。
在R上为减函数(2)求实数k的取值范围。
设椭圆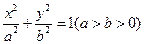 的左焦点为F,上顶点为A,直线
的左焦点为F,上顶点为A,直线 AF的倾斜角为
AF的倾斜角为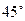 (1)求椭圆的离心率;(2)设过点A且与AF垂直的直线与椭圆右准线的交点为B,过A、B、F三点的圆M恰好与直线
(1)求椭圆的离心率;(2)设过点A且与AF垂直的直线与椭圆右准线的交点为B,过A、B、F三点的圆M恰好与直线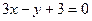 相切,求椭圆的方程及圆M的方程
相切,求椭圆的方程及圆M的方程
已知函数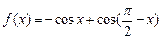 ,
,
(1)若 ,求函数
,求函数 的最大值与最小值及此时x的值;
的最大值与最小值及此时x的值;
(2)若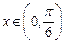 ,且
,且 ,求
,求 的值.
的值.
如图,某小区准备绿化一块直径为 的半圆形空地,
的半圆形空地,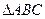 外的地方种草,
外的地方种草,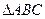 的内接正方形
的内接正方形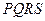 为一水池,其余地方种花.若
为一水池,其余地方种花.若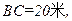
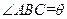 ,设
,设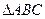 的面积为
的面积为 ,正方形
,正方形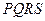 的面积为
的面积为 ,将比值
,将比值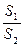 称为“规划合理度”.
称为“规划合理度”.
(1)试用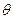 表示
表示 和
和 .(2)当
.(2)当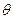 变化时,求“规划合理度”取得最小值时的角
变化时,求“规划合理度”取得最小值时的角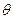 的大小.
的大小.