若数列an的前n项和Snn210nn1,2,3,…，则此数列-优题课

题文

若数列 $\{a_{n}\}$ 的前 $n$ 项和 $S_{n} = n^{2} - 10 n (n = 1, 2, 3, \dots)$ ，则此数列的通项公式为；数列 $\{n a_{n}\}$ 中数值最小的项是第项．

科目数学题型填空题难度较难

相关试题

设 $\{a_{n}\}$ 是公比为 $q$ 的等比数列， $|q < 1|$ ，令 $b_{n} = a_{n} + 1 (n = 1, 2 \dots \dots)$ ，若数列 $\{b_{n}\}$ 有连续四项在集合 $\{- 53, - 23, 19, 37, 82\}$ 中，则 $6 q$ = .

如图，在平面直角坐标系 $x o y$ 中， $A_{1}, A_{2}, B_{1}, B_{2}$ 为椭圆 $\frac{x^{_{2}}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1 (a > b > 0)$ 的四个顶点， $F$ 为其右焦点，直线 $A_{1} B_{2}$ 与直线 $B_{1} F$ 相交于点T，线段 $O T$ 与椭圆的交点 $M$ 恰为线段 $O T$ 的中点，则该椭圆的离心率为.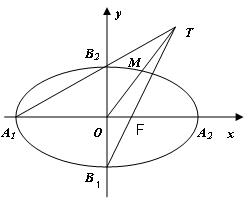

设 $α$ 和 $β$ 为不重合的两个平面，给出下列命题：
（1）若 $α$ 内的两条相交直线分别平行于 $β$ 内的两条直线，则 $α$ 平行于 $β$ ；
（2）若 $α$ 外一条直线 $l$ 与 $α$ 内的一条直线平行，则 $l$ 和 $α$ 平行；
（3）设 $α$ 和 $β$ 相交于直线 $l$ ，若 $α$ 内有一条直线垂直于 $l$ ，则 $α$ 和 $β$ 垂直；
（4）直线 $l$ 与 $α$ 垂直的充分必要条件是 $l$ 与 $α$ 内的两条直线垂直.
上面命题中，真命题的序号 .（写出所有真命题的序号）

已知集合 $A = {x | \log_{2} x \leq 2}, B = (- \infty, a)$ ，若 $A \subseteq B$ 则实数 $a$ 的取值范围是 $(c, + \infty)$ ，其中 $c$ = .

已知 $a = \frac{\sqrt{5} - 1}{2}$ ，函数 $f (x) = a^{x}$ ，若实数 $m$ 、 $n$ 满足 $f (m) > f (n)$ ，则 $m$ 、 $n$ 的大小关系为.

试卷网试题网古诗词网作文网范文网