某中学号召学生在今年春节期间至少参加一次社会公益活动(以下简称活动).该校合唱团共有100名学生,他们参加活动的次数统计如图所示.

(I)求合唱团学生参加活动的人均次数;
(II)从合唱团中任意选两名学生,求他们参加活动次数恰好相等的概率.
(III)从合唱团中任选两名学生,用
表示这两人参加活动次数之差的绝对值,求随机变量
的分布列及数学期望
.
(本小题满分14分,第1小题满分6分,第2小题满分8分)
野营活动中,学生在平地上用三根斜杆搭建一个正三棱锥形的三脚支架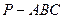 (如图3)进行野炊训练. 已知
(如图3)进行野炊训练. 已知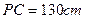 ,
,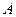 、
、 两点间距离为
两点间距离为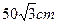 .
.
(1)求斜杆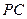 与地面
与地面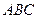 所成角的大小(用反三角函
所成角的大小(用反三角函 数值表示)
数值表示) ;
;
(2)将炊事锅看作一个点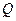 ,用吊绳
,用吊绳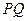 将炊事锅吊起烧水(锅的大小忽略不计),若使炊事锅
将炊事锅吊起烧水(锅的大小忽略不计),若使炊事锅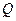 到地面
到地面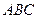 及各条斜杆的距离都不小于30
及各条斜杆的距离都不小于30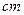 ,试问吊绳
,试问吊绳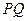 长的取值范围.
长的取值范围.
(本小题满分14分,第1小题满分6分,第2小题满分8分)
已知向量 ,其中
,其中 且
且 ,
,
(1)当 为何值时,
为何值时, ;
;
(2)解关于x的不等式 .
.
(本小题满分12分)
已知函数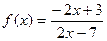 ,若存在实数
,若存在实数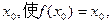 则称
则称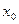 是函数
是函数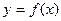 的一个不动点.
的一个不动点.
(I)证明:函数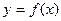 有两个不动点;
有两个不动点;
(II)已知a、b是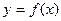 的两个不动点,且
的两个不动点,且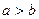 .当
.当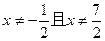 时,比较
时,比较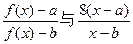 的大小;
的大小;
(III)在数列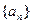 中,
中,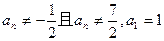 ,等式
,等式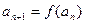 对任何正整数n都成立,求数列
对任何正整数n都成立,求数列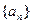 的通项公式.
的通项公式.
(本小题满分12分)
已知函数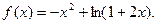
(I)求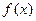 的最大值;
的最大值;
(II)设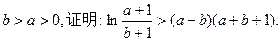
(本小题满分12分)
已知实轴长为2a,虚轴长为2b的双曲线S的焦点在x轴上,直线 是双曲线S的一条渐近线,而且原点O,点A(a,0)和点B(0,-b)使等式
是双曲线S的一条渐近线,而且原点O,点A(a,0)和点B(0,-b)使等式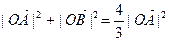 ·
·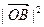 成立.
成立.
(I)求双曲线S的方程;
(II)若双曲线S上存在两个点关于直线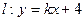 对称,求实数k的取值范围.
对称,求实数k的取值范围.