设数列 满足 .
(I)求数列 的通项;   (II)设 求数列 的前 项和 .
已知函数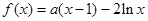 (d为常数)
(d为常数)
(1)当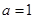 对,求
对,求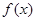 单调区间;
单调区间;
(2)若函数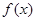 在区间(0,1)上无零点,求a的最大值.
在区间(0,1)上无零点,求a的最大值.
己知曲线 与x袖交于A,B两点,点P为x轴上方的一个动点,点P与A,B连线的斜率之积为-4
与x袖交于A,B两点,点P为x轴上方的一个动点,点P与A,B连线的斜率之积为-4
(1)求动点P的轨迹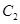 的方程;
的方程;
(2)过点B的直线 与
与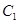 ,
,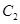 分别交于点M ,Q(均异于点A,B),若以MQ为直径的圆
分别交于点M ,Q(均异于点A,B),若以MQ为直径的圆
经过点A,求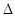 AMQ的面积.
AMQ的面积.
己知四棱锥P-ABCD,其中底面ABCD为矩形侧棱PA 底面ABCD,其中BC=2,AB=2PA=6,
底面ABCD,其中BC=2,AB=2PA=6,
M,N为侧棱PC上的两个三等分点,如图所示:
(1)求证:AN∥平面MBD;
(2)求二面角B-PC-A的余弦值.
设X为随机变量,从棱长为a的正方体 ,的八个顶点中任取四个点,当四点共面时,X=0;当四点不共面时,X的值为四点组成的四面体的体积.
,的八个顶点中任取四个点,当四点共面时,X=0;当四点不共面时,X的值为四点组成的四面体的体积.
(1)求概率P(X=0);
(2)求X的分布列,并求其数学期望E(X).
在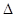 ABC中,记角A,B,C的对边为a,b,c,角A为锐角,设向量
ABC中,记角A,B,C的对边为a,b,c,角A为锐角,设向量
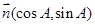 ,且
,且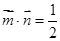 .
.
(1)求角A的大小及向量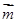 与
与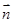 的夹角;
的夹角;
(2)若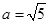 ,求
,求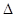 ABC面积的最大值.
ABC面积的最大值.