设函数
,其中
为实数.
(Ⅰ)若
的定义域为
,求
的取值范围;
(Ⅱ)当
的定义域为
时,求
的单减区间.
假设关于某设备的使用年限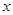 和所支出的维修费用
和所支出的维修费用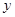 (万元),有如下的统计资料:
(万元),有如下的统计资料:
使用年限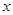 |
2 |
3 |
4 |
5 |
6 |
维修费用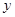 |
2.2 |
3.8 |
5.5 |
6.5 |
7.0 |
若由资料知道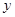 对
对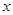 呈线性相关关系.
呈线性相关关系.
附: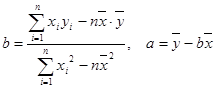
试求:
(1)线性回归方程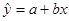 的回归系数.
的回归系数.
(2)估计使用年限为10年时,维修费用是多少?
已知函数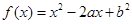 ,
,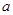 ,
,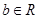 .
.
(1)若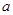 从集合{0,1,2,3}中任取一个元素,
从集合{0,1,2,3}中任取一个元素,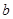 从集合{0,1,2}中任取一个元素,求方程
从集合{0,1,2}中任取一个元素,求方程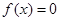 有两个不相等实根的概率;
有两个不相等实根的概率;
(2)若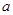 从区间
从区间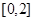 中任取一个数,
中任取一个数,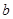 从区间
从区间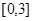 中任取一个数,求方程
中任取一个数,求方程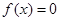 没有实根的概率.
没有实根的概率.
某市2013年4月1日—4月30日对空气污染指数的监测数据如下(主要污染物为可吸入颗粒物):
61,76,70,56,81,91,92,91,75,81,88,67,101,103,95,91,77,86,81,83,82,82,64,79,86,85,75,71,49,45,
(1)完成频率分布表;
(2)作出频率分布直方图;
一扇形周长为60,则它的半径和圆心角各为多少时扇形面积最大?最大是多少?
在添加剂的搭配使用中,为了找到最佳的搭配方案,需要对各种不同的搭配方式作比较.在试制某种牙膏新品种时,需要选用两种不同的添加剂.现有芳香度分别为0,1,2,3,4,5的六种添加剂可供选用.根据试验设计原理,通常首先要随机选取两种不同的添加剂进行搭配试验.(写解题过程)
(1)求所选用的两种不同的添加剂的芳香度之和等于4的概率;
(2)求所选用的两种不同的添加剂的芳香度之和不小于3的概率.