（本小题满分1５分）
如图，设抛物线C：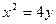
的焦点为F，
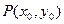为抛物线上的任一点（其中
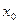≠0），[
过P点的切线交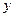
轴于Q点．
（Ⅰ）证明：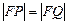
；
（Ⅱ）Q点关于原点O的对称点为M，过M点作平行于PQ的直线
交抛物线C于A、B两点，若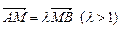
，求
的值．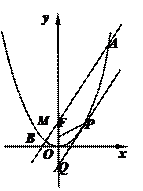
（ 12分 ）已知二次函数f(x)=
，x∈[－1,2]
(1)求函数f(x)的最小值
；
(2)若f(x)≥－1恒成立，求t的取值范围．
（ 12分 ）已知集合A={x|x2－3x+2=0},B={x|x2－ax+3a－5=0},若A∩B=B，求实数a的值
（ 12分 ）求经过A(-2，-4)且与直线l:x+3y-26=0相切于点B(8，6)的圆的方程.
（ 14分 ）已知圆C：x2+y2-2x+4y-4=0,是否存在斜率为1的直线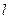
,使以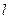被圆C所截得的弦AB为直径的圆经过原点？若存在,写出直线的方程；若不存在,请说明理由.
（ 12分 ）如图,已知三棱锥A-BPC中,AP⊥PC,AC⊥BC,M为AB中点,D为PB中点,且△PMB为正三角形. 
(1)求证:DM∥平面APC;
(2)求证:平面ABC⊥平面APC;
(3)若BC=4,AB=20,求三棱锥D-BCM的体积.