( 12分 )如图,已知三棱锥A-BPC中,AP⊥PC,AC⊥BC,M为AB中点,D为PB中点,且△PMB为正三角形. 
(1)求证:DM∥平面APC;
(2)求证:平面ABC⊥平面APC;
(3)若BC=4,AB=20,求三棱锥D-BCM的体积.
已知过点(0,1)的直线l与曲线C: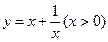 交于两个不同点M和N。求曲线C在点M、N处切线的交点轨迹。
交于两个不同点M和N。求曲线C在点M、N处切线的交点轨迹。
设集合P={1,2,3,4,5},对任意k∈P和正整数m,记f(m,k)=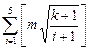 ,其中[a]表示不大于a的最大整数。求证:对任意正整数n,存在k∈P和正整数m,使得f(m,k)=n。
,其中[a]表示不大于a的最大整数。求证:对任意正整数n,存在k∈P和正整数m,使得f(m,k)=n。
如图,在7×8的长方形棋盘的每个小方格的中心点各放一个棋子。如果两个棋子所在的小方格共边或共顶点,那么称这两个棋子相连。现从这56个棋子中取出一些,使得棋盘上剩下的棋子,没有五个在一条直线(横、竖、斜方向)上依次相连。问最少取出多少个棋子才可能满足要求?并说明理由。
设 ,求证:当正整数n≥2时,an+1<an。
,求证:当正整数n≥2时,an+1<an。
设x1,x2是关于x的一元二次方程x2-2(m-1)x+m+1=0的两个实根,又y=x21+x22,求y=f(m)的解析式及此函数的定义域.