选修4—5：不等式选讲
已知a，b为正数，求证：
.
(本题满分12分)
投掷飞碟的游戏中，飞碟投入红袋记2分，投入蓝袋记1分，未投入袋记0分.现知某人在以前投掷1000次的试验中，有500次入红袋，250次入蓝袋，其余不能入袋
（1）求该人在4次投掷中恰有三次投入红袋的概率;
（2） 求该人两次投掷后得分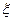
的分布列和数学期望.
(本题满分12分)，
如图，菱形ABCD所在平面与矩形ACEF所在平面互相垂直，已知BD=
AF，且点M是线段EF的中点.
（1）求证：AM∥平面BDE；
（2）求平面DEF与平面BEF所成的角.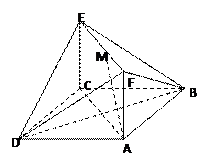
（本小题满分12分）
已知向量
，函数
．求：
（1）函数
的最小值；
（2）函数的单调递
增区间．
（本小题满分12分）已知函数
的图象在点
处的切线方程为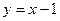
．
（1）用
表示出
；
（2）若
在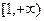
上恒成立，求的取值范围；
（3）证明：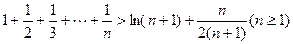
．
（本小题满分12分）已知函数
，其中
．
（1）若
在x=1处取得极值，求a的值；
（2）求的单调区间；
（3）若的最小值为1，求a的取值范围．