现有两组卡片，每组3张，牌面数字分别是1、2、3，从中各摸一张。
（1）求摸出2张的牌面数字之和等于4的概率。
（2）摸出2张的牌面数字之和为多少时的概率最大？
（本小题满分12
分）
设函数f(x)的定义域为R，若|f(x)|≤|x|对任意的实数x均成立，则称函数f(x)为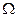
函数。
（1）试判断函数
=
=
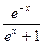中哪些是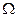函数，并说明理由；
（2）求证：若a>1，则函数f(x)=ln(x2+a)-lna是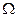函数。
（本小题满分12分）
将如图1的直角梯形ABEF（图中数字表示对应线段的长度）沿直线CD折成直二面角，连结EB、FB、FA后围成一个空间几何体如图2所示，
（1）求异面直线BD与EF所成角的大小；
（2）求二面角D—BF—E的大小；
（3）求这个几何体的体积.
（本小题满分12分）
从集合
的所有非空真子集中等可能地取出一个.
（1）求所取的子集中元素从小到大排列成等
比数列的概率；
（2）记所取出的子集的元素个数为
，求的分布列和数学期望.
（本小题满分12分）
在锐角△ABC
中，已知内角
A、B、C的对边分别为a、b、c.向量
，
,且向量
、
共线。
（1）求角B的大小；
（2）如果b=1,求△ABC的面积S△ABC的最大值。
(本小题共13分)
设集合
，对于
，记
且
，由所有
组成的集合设为
．
（Ⅰ）求
的值；
（Ⅱ）设集合
，对任意
，试求
；
（Ⅲ）设，试求
的概率．