设集合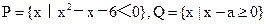
(1)设P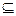 Q,求实数a的取值范围.
Q,求实数a的取值范围.
(2)若P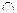 Q=
Q= ,求实数a的取值范围
,求实数a的取值范围
等差数列{an}的各项均为正数,a1=3,前n项和为Sn,{bn}为等比数列,b1=1,且b2S2=64,b3S3=960.
(1)求an与bn;
(2)求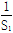 +
+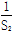 +…+
+…+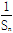 .
.
已知函数 在区间
在区间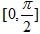 上的最大值为2.
上的最大值为2.
(1)求常数m的值;
(2)在△ABC中,角A、B、C所对的边是a、b、c,若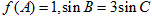 ,△ABC面积为
,△ABC面积为 .求边长a.
.求边长a.
在平面直角坐标系中, 为坐标原点,已知曲线
为坐标原点,已知曲线 上任意一点
上任意一点 (其中
(其中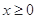 )到定点
)到定点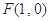 的距离比它到
的距离比它到 轴的距离大1.
轴的距离大1.
(1)求曲线 的轨迹方程;
的轨迹方程;
(2)若过点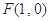 的直线
的直线 与曲线
与曲线 相交于A、B不同的两点,求
相交于A、B不同的两点,求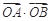 的值;
的值;
(3)若曲线 上不同的两点
上不同的两点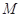 、
、 满足
满足 ,求
,求 的取值范围.
的取值范围.
在平面直角坐标系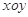 中,点
中,点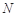 与点
与点 关于原点
关于原点 对称,
对称, 是动点,且直线
是动点,且直线 与
与
的斜率之积等于 .
.
(Ⅰ)求动点 的轨迹方程;
的轨迹方程;
(Ⅱ)设直线 和
和 与直线
与直线 分别交于
分别交于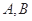 两点,问:是否存在点
两点,问:是否存在点 使得
使得 与
与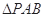 的面
的面
积相等?若存在,求出点 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
已知函数 (
(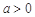 且
且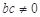 ).
).
(Ⅰ)若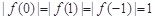 ,试求
,试求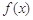 的解析式;
的解析式;
(Ⅱ)令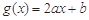 ,若
,若 ,又
,又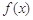 的图像在
的图像在 轴上截得的弦的长度为
轴上截得的弦的长度为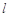 ,且
,且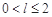 ,试比较
,试比较 、
、 的大小.
的大小.