已知aÎR，函数f（x）=x| x－a |．
（1）当a=2时，求使f（x）=x成立的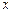
的集合；
（2）求函数y=f（x）在区间
上的最小值．
已知直线
经过点
，
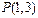且与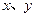
轴的正半轴交于
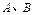两点，求
取
最小值时直线的方程.
如图，已知△ABC是边长为1的正三角形，M、N分别是边AB、AC上的点，线段MN经过△ABC的中心G，设Ð
MGA＝a（
）.
（1）试将△AGM、△AGN的面积（分别记为S1与S2）表示为a的函数;
（2）求y＝
的最大值与最小值.
求实数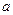
的取值范围，使不等式
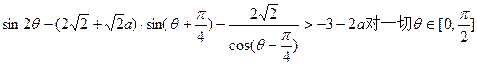恒成立.
已知函数f(x)=A
(A>0,
>0,0<
<
，且y=f(x)的最大值为2，其
图象相邻两对称轴间的距离为2，并过点（1，2）.
（1）求;
（2）计算f (1) + f (2) +… + f ( 2 008 ).
已知函数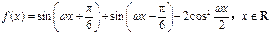
（其中
）
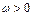（1）求函数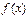
的值域；
（2）若函数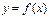
的图象与直线
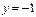的两个相邻交点间的距离为
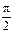，求函数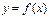的单调增区间．