(本小题满分12分)
已知函数 R).
R).
(Ⅰ)若a=1,函数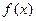 的图象能否总在直线
的图象能否总在直线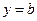 的下方?说明理由;
的下方?说明理由;
(Ⅱ)若函数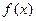 在(0,2)上是增函数,求a的取值范围;
在(0,2)上是增函数,求a的取值范围;
(Ⅲ)设 为方程
为方程 的三个根,且
的三个根,且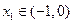 ,
, ,
, , 求证:
, 求证: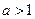 或
或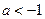
分别指出下列复合命题的形式及构成它的简单命题:
(1)3是质数或合数.
(2)他是运动员兼教练员.
(3)相似三角形不一定是全等三角形.
你能写出下列命题p的非(否定)吗?
(1)p:100既能被4整除又能被5整除
(2)p:三条直线两两相交
(3)p:一元二次方程至多有两个解
(4)p:
函数 的定义域为集合
的定义域为集合 ,函数
,函数 的定义域为集合
的定义域为集合 . (1)判定函数
. (1)判定函数 的奇偶性,并说明理由.
的奇偶性,并说明理由.
(2)问: 是
是 的什么条件(充分非必要条件 、必要非充分条件、充要条件、既非充分也非必要条件)? 并证明你的结论.
的什么条件(充分非必要条件 、必要非充分条件、充要条件、既非充分也非必要条件)? 并证明你的结论.
已知:a、b、c是互不相等的非零实数.
求证:三个方程ax2+2bx+c=0,bx2+2cx+a=0,cx2+2ax+b=0至少有一个方程有两个相异实根.
已知 :
: ,
, :
:
且 是
是 的必要不充分条件,求实数
的必要不充分条件,求实数 的取值范围。
的取值范围。