为了了解《中华人民共和国道路交通安全法》在学生中的普及情况 ,调查部门对某校5名学生进行问卷调查,5人得分情况如下:6,7,8,9,10。把这5名学生的得分看成一个总体。
(1)求该总体的平均数;
(2)用简单随机抽样方法从这5名学生中抽取2名,他们的得分组成一个样本,求该样本平均数与总体平均数之差的绝对值超过0.5的概率。
如图,在四棱锥PABCD中,PD⊥平面ABCD,四边形ABCD是菱形,AC=2,BD=2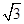 ,E是PB上任意一点.
,E是PB上任意一点.
(1)求证:AC⊥DE;
(2)已知二面角APBD的余弦值为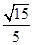 ,若E为PB的中点,求EC与平面PAB所成角的正弦值.
,若E为PB的中点,求EC与平面PAB所成角的正弦值.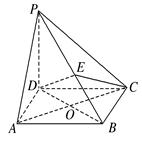
中国2010年上海世博会已于2010年5月1日在上海隆重开馆.小王某天乘火车从重庆到上海去参观世博会,若当天从重庆到上海的三列火车正点到达的概率分别为0.8、0.7、0.9,假设这三列火车之间是否正点到达互不影响.求:
(1)这三列火车恰好有两列正点到达的概率;
(2)这三列火车至少有一列正点到达的概率
已知向量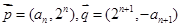 ,n∈N*,向量
,n∈N*,向量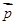 与
与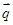 垂直,且a1=1.
垂直,且a1=1.
(1)求数列{an}的通项公式;
(2)若数列{bn}满足bn=log2an+1,求数列{an·bn}的前n项和Sn.
已知函数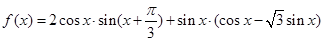
(1)求函数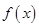 的最小正周期和单调递减区间;
的最小正周期和单调递减区间;
(2)在 中,
中,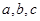 分别是角A、B、C的对边,若
分别是角A、B、C的对边,若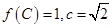 ,求
,求 面积的最大值.
面积的最大值.
已知数列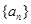 的前
的前 项和为
项和为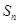 ,且
,且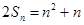 2.
2.
(1)求数列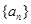 的通项公式;
的通项公式;
(2)若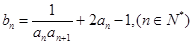 求数列
求数列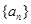 的前
的前 项和
项和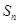 .
.