已知向量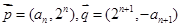 ,n∈N*,向量
,n∈N*,向量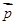 与
与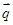 垂直,且a1=1.
垂直,且a1=1.
(1)求数列{an}的通项公式;
(2)若数列{bn}满足bn=log2an+1,求数列{an·bn}的前n项和Sn.
等比数列{an}的各项均为正数,且 。
。
(1)求数列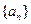 的通项公式;
的通项公式;
(2)设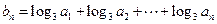 ,求数列
,求数列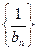 的前
的前 项和.
项和.
已知函数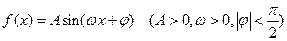 的图象与
的图象与 轴
轴
的交点为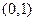 ,它在
,它在 轴右侧的第一个最高点和第一个最低点的坐标分别为
轴右侧的第一个最高点和第一个最低点的坐标分别为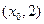 和
和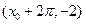 .
.
(1)求 的解析式及
的解析式及 的值;
的值;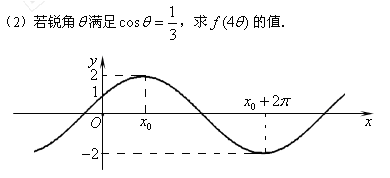
(本小题满分15分)已知二次函数 对
对 都满足
都满足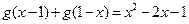 且
且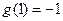 ,设函数
,设函数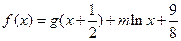
( ,
,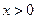 ).
).
(1)求 的表达式;
的表达式;
(2)若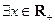 ,使
,使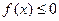
 成立,求实数
成立,求实数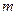 的取值范围;
的取值范围;
(3)设 ,
, ,求证:对于
,求证:对于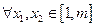 ,恒有
,恒有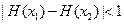 .
.
(本小题满分12分)已知函数f(x)=2x-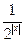 .
.
(1)若f(x)=2,求x的值;
(2)若2tf(2t)+mf(t)≥0对于t∈[1,2]恒成立,求实数m的取值范围.
(本小题满分12分)已知△ABC的面积S满足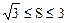 , 且
, 且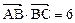 ,
, 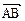 与
与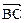 的夹角为
的夹角为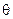 .
.
(I) 求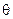 的取值范围;
的取值范围;
(II)求函数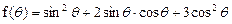 的最小值.
的最小值.