在公差为
 的等差数列
的等差数列 和公比为
和公比为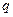 的等比数列
的等比数列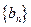 中,已知
中,已知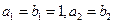 ,
,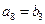 .
.
(Ⅰ)求数列 与
与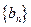 的通项公式;
的通项公式;
(Ⅱ)是否存在常数 ,使
,使 得对于一切正整数
得对于一切正整数 ,都有
,都有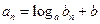 成立?若存在,求出常数
成立?若存在,求出常数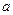 和
和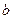 ,若不存在说明理由
,若不存在说明理由
在水流速度大小为10km/h的河中,如果要使船实际以10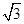 km/h大小的速度与河岸成直角横渡,求船行驶速度的大小与方向.
km/h大小的速度与河岸成直角横渡,求船行驶速度的大小与方向.
已知两个力F1、F2的方向互相垂直,且它们的合力F大小为10N,与力F1的夹角是60°,求力F1、F2的大小.
设a表示“向西走2km”,b表示“向北走2km”,则a+b表示向哪个方向行走了多少?
已知函数f(x)=Acos(ωx+φ)+b(A>0,ω>0,|φ|< )在同一个周期内的图象上有一个最大值点A
)在同一个周期内的图象上有一个最大值点A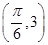 和一个最小值点B
和一个最小值点B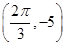 .
.
(1)求f(x)的解析式;
(2)经过怎样的平移和伸缩变换可以将f(x)的图象变换为g(x)=cosx的图象.
已知函数f(x)=2sin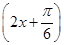 +a(其中a为常数).
+a(其中a为常数).
(1)求f(x)的单调区间;
(2)当x∈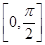 时,f(x)的最大值为4,求a的值;
时,f(x)的最大值为4,求a的值;
(3)求出使f(x)取最大值时x的取值集合.