已知函数f(x)=Acos(ωx+φ)+b(A>0,ω>0,|φ|< )在同一个周期内的图象上有一个最大值点A
)在同一个周期内的图象上有一个最大值点A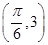 和一个最小值点B
和一个最小值点B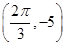 .
.
(1)求f(x)的解析式;
(2)经过怎样的平移和伸缩变换可以将f(x)的图象变换为g(x)=cosx的图象.
如图,现在要在一块半径为1m。圆心角为60°的扇形纸板AOB上剪出一个平行
四边形MNPQ,使点P在AB弧上,点Q在OA上,点M,N在OB上,设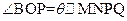 的
的
面积为S。
(1)求S关于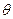 的函数
的函数 关系式;
关系式;
(2)求S的最大值及相应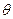 的值
的值
已知向量
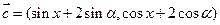 ,其中
,其中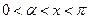 (1)若
(1)若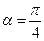 。求函数
。求函数 的最小值及相应x的值;(2)若
的最小值及相应x的值;(2)若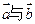 的
的
夹角为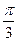 ,且
,且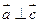 ,求
,求 的值。
的值。
已知向量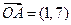 ,
,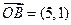 ,
, ,点
,点 为直线
为直线 上一动点.
上一动点.
(Ⅰ)求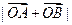 ;
;
(Ⅱ)当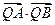 取最小值时,求
取最小值时,求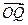 的坐标.
的坐标.
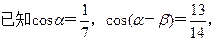

求: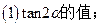
 .
.
某商场为吸引顾客消费推出一项优惠活动.活动规则如下:消费每满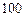 元可以
元可以
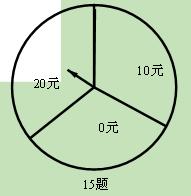
转动如图所示的圆盘一次,其中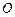 为圆心,且标有
为圆心,且标有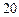 元、
元、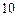 元、
元、 元的三部分区域面积相
元的三部分区域面积相
等. 假定指针停在任一位置都是等可能的.当指针停在某区域时,返相应金额的优惠券.(例
如:某顾客消费了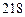 元,第一次转动获得了
元,第一次转动获得了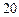 元,第二次获得了
元,第二次获得了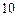 元,则其共获得了
元,则其共获得了
元 优惠券.)顾客甲和乙都到商场进行了消费,并按照规则参与了活动.
优惠券.)顾客甲和乙都到商场进行了消费,并按照规则参与了活动.
⑴若顾客甲消费了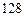 元,求他获得优惠券面额大于
元,求他获得优惠券面额大于 元的概率?
元的概率?
⑵若顾客乙消费了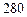 元,求他
元,求他 总共获得优惠券金额不低于
总共获得优惠券金额不低于 元的概率?
元的概率?