已知向量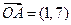 ,
,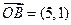 ,
, ,点
,点 为直线
为直线 上一动点.
上一动点.
(Ⅰ)求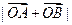 ;
;
(Ⅱ)当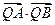 取最小值时,求
取最小值时,求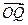 的坐标.
的坐标.
(本小题满分12分) 如图,在四棱锥 中,底面
中,底面 是正方形,侧棱
是正方形,侧棱 ⊥底面
⊥底面 ,
, ,
, 是
是 的中点,作
的中点,作 交
交 于点
于点
(1) 证明 //平面
//平面 ;
;
(2) 证明 ⊥平面
⊥平面 ;
;
(3) 求二面角 —
— —
— 的大小。
的大小。
(本小题满分8分)如图四边形 为梯形,
为梯形, ,
, ,求图中阴影部分绕
,求图中阴影部分绕 旋转一周所形成的几何体的表面积和体积。
旋转一周所形成的几何体的表面积和体积。
(本小题满分8分)已知直线 经过点
经过点 ,且垂直于直线
,且垂直于直线 ,
,
(1)求直线 的方程;(2)求直线
的方程;(2)求直线 与两坐标轴围成三角形的面积。
与两坐标轴围成三角形的面积。
(本小题满分12分)如图,正方体ABCD—A1B1C1D1中,P、M、N分别为棱DD1、AB、BC的中点 .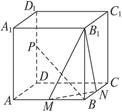
(1)求二面角B1MNB的正切值;
(2)求证:PB⊥平面MNB1;
(3)若正方体的棱长为1,画出一个正方体表面展开图,使其满足“有4个正方形面相连成一个长方形”的条件,并求出展开图中P、B两点间的距离 .
(本小题满分12分)如图, 在直角梯形 中,
中,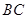 ∥
∥
点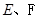 分别是
分别是 的中点,现将
的中点,现将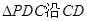 折起,使
折起,使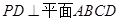 ,
,
(1)求证: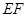 ∥平面
∥平面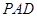 ;
;
(2)求点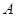 到平面
到平面 的距离.
的距离.