某射手每次射击击中目标的概率是
，且各次射击的结果互不影响.
(Ⅰ)假设这名射手射击5次，求恰有2次击中目标的概率
(Ⅱ)假设这名射手射击5次，求有3次连续击中目标，另外2次未击中目标的概率
(Ⅲ)假设这名射手射击3次，每次射击，击中目标得1分，未击中目标得0分，在3次射击中，若有2次连续击中，而另外1次未击中，则额外加1分；若3次全击中，则额外加3分，记ξ为射手射击3次后的总得分数，求ξ的分布列
已知函数f（x）的定义域为{x| x ≠ kπ，k ∈ Z}，且对于定义域内的任何x、y，有f（x-y） = 成立，且f（a） = 1（a为正常数），当0 < x < 2a时，f（x） > 0．
（1）判断f（x）奇偶性；
（2）证明f（x）为周期函数；
（3）求f（x）在[2a，3a] 上的最小值和最大值．
已知数列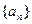
满足：
，且
（
）． 
（1）求证：数列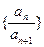
为等差数列；
（2）求数列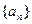的通项公式；
（3）求右表中前
行所有数的和
．
已知抛物线
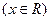与坐标轴有三个交点，经过这三点的圆记为
.
（1）求实数
的取值范围；
（2）设抛物线与ｘ轴的交点从左到右分别为A、B，与ｙ轴的交点为C，求A、B、C三点的坐标；
（3）设直线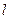
是抛物线在点A处的切线，试判断直线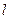是否也是圆的切线？并说明理由.
某工厂生产甲、乙两种产品，每种产品都是经过第一和第二工序加工而成，两道工序的加工结果相互独立，每道工序的加工结果均有A、B两个等级.对每种产品，两道工序的加工结果都为A级时，产品为一等品，其余均
为二等品.
（1）已知甲、乙两种产品每一道工序的加工结
果为A级的概率如表一所示，分别求生产
出的甲、乙产品为一等品的概率P甲、P乙；
（2）已知一件产品的利润如表二所示，用ξ、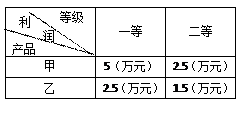
η分别表示一件甲、乙产品的利润，在
（1）的条件下，求ξ、η的分布列及Eξ、
Eη；
（3）已知生产一件产品需用的工人数和资金额
如表三所示.该工厂有工人40名，可用资.
|
金60万元.设x、y分别表示生产甲、乙产
|
品的数量，在（2）的条件下，x、y为何
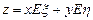最大？最大值是多少？
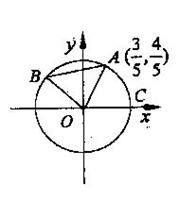如图A、B是单位圆Ｏ上的点，且B在第二象限，C是圆与x轴正半轴的交点，A点的坐标为
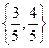，△AOB为正三角形.
（1）求sin∠COA的值；
（2）求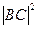
的值.