在立体图形P－ABCD中，底面ABCD是一个直角梯形，∠BAD＝90°，AD∥BC，
AB＝BC＝a，AD=PA＝2a，E是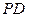
边的中点，且PA⊥底面ABCD。
（1）求证：BE⊥PD
（2）求证：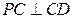
（3）求异面直线AE与CD所成的角．
(本小题满分12分)已知数列{an}满足a1＝1，an>0，Sn是数列{an}的前n项和，对任意n∈N＋，有2Sn＝p(2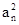
＋an－1)(p为常数)．
(1)求p和a2，a3的值；
(2)求数列{an}的通项公式．
已知正方体
，
是底面
对角线的交点.
（1）求直线
和平面
所成的角；
（2）求证：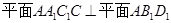
．
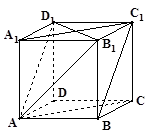
(本小题满分12分)设{an}是等差数列，{bn}是各项都为正数的等比数列，且a1=b1=1，a3+b5=21，a5+b3=13.
(1)求{an}，{bn}的通项公式；
(2)求数列
的前n项和Sn.
(本小题满分12分)数列
是递增的等比数列，且
（1）求数列
的通项公式；
（2）若
，求证:数列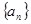
是等差数列.
(本小题满分10分)等差数列
的前
项和记为
，已知
(1)求通项
；
（2）若
求.