(本小题满分12分)
将一颗质地均匀的正方体骰子(六个面的点数分别为1,2,3,4,5,6)先后抛掷两次,记第一次出现的点数为 ,第二次出现的点数为
,第二次出现的点数为 ,设复数
,设复数 .
.
(Ⅰ)求事件“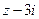 ”为实数”的概率;
”为实数”的概率;
(Ⅱ)求事件“ ”的概率.
”的概率.
已知四棱锥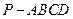 的底面是菱形.
的底面是菱形.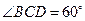 ,
,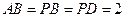 ,
,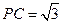 ,
,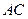 与
与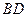 交于
交于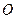 点,
点,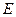 ,
,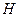 分别为
分别为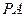 ,
,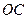 的中点.
的中点. (Ⅰ)求证:
(Ⅰ)求证: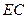 ∥平面
∥平面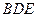 ;
;
(Ⅱ)求证: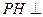 平面
平面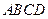 ;
;
(Ⅲ)求直线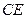 与平面
与平面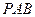 所成角的正弦值
所成角的正弦值
在△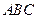 中,角
中,角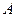 ,
,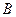 ,
,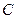 的对边分别为
的对边分别为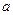 ,
,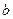 ,
,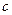 分,且满足
分,且满足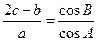 .
.
(Ⅰ)求角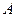 的大小;
的大小;
(Ⅱ)若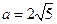 ,求△
,求△ 面积的最大值
面积的最大值
(本小题15分)
如图在三棱锥P-ABC中,PA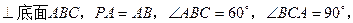
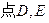 分别在棱
分别在棱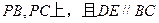 ,
,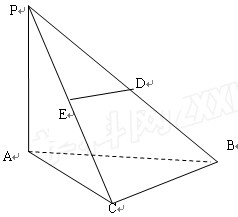
(1)求证:BC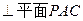
(2)当D为PB中点时,求AD与平面PAC所成的角的余弦值;
(3)是否存在点E,使得二面角A-DE-P为直二面角,并说明理由。
(本小题15分)
已知函数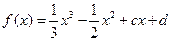 有极值.
有极值.
(1)求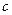 的取值范围;
的取值范围;
(2)若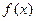 在
在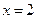 处取得极值,且当
处取得极值,且当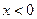 时,
时,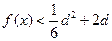 恒成立,求
恒成立,求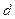 的取值范围.
的取值范围.
(本小题14分)
如图,在四棱锥V-ABCD中底面ABCD是正方形,侧面VAD是正三角形,
平面VAD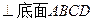
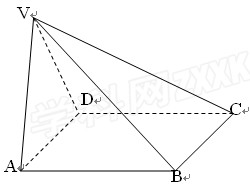
(1)证明:AB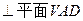 ;
;
(2)求面VAD与面VDB所成的二面角的余弦值。