(本小题满分14分)椭圆E的中心在原点O,焦点在x轴上,离心率 ,过点C(-1,0)的直线l交椭圆于A、B两点,且满足:
,过点C(-1,0)的直线l交椭圆于A、B两点,且满足: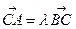 (λ≥2)。
(λ≥2)。
(1)若λ为常数,试用直线l的斜率k(k≠0)表示三角形OAB的面积;
(2)若λ为常数,当三角形OAB的面积取得最大值时,求椭圆E的方程;
(3)若λ变化,且λ=k2+1,试问:实数λ和直线l的斜率k(k∈R)分别为何值时,椭圆E的短半轴长取得最大值?并求出此时的椭圆方程。
【原创】选修4 - 1:几何证明选讲如图,△ABC内接于⊙O,点D在OC的延长线上,AD与⊙O相切,割线DM与⊙O相交于点M,N,若∠B=30°,AC=1,求DM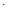 DN
DN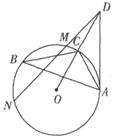
等差数列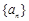 的前
的前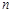 项和为
项和为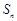 ,已知
,已知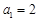 ,
,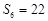 .
.
(1)求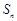 ;
;
(2)若从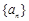 中抽取一个公比为
中抽取一个公比为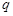 的等比数列
的等比数列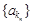 ,其中
,其中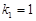 ,且
,且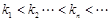 ,
,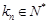 .
.
①当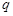 取最小值时,求
取最小值时,求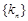 的通项公式;
的通项公式;
②若关于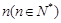 的不等式
的不等式 有解,试求
有解,试求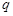 的值.
的值.
已知函数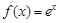 ,
,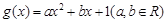 .
.
(1)若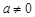 ,则
,则 ,
,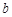 满足什么条件时,曲线
满足什么条件时,曲线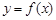 与
与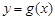 在
在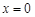 处总有相同的切线?
处总有相同的切线?
(2)当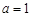 时,求函数
时,求函数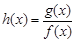 的单调减区间;
的单调减区间;
(3)当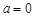 时,若
时,若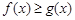 对任意的
对任意的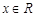 恒成立,求
恒成立,求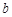 的取值的集合.
的取值的集合.
【原创】已知椭圆C :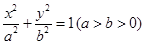 , 经过点P
, 经过点P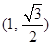 ,离心率是
,离心率是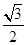 .
.
(1)求椭圆C的方程;
(2)设直线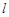 与椭圆
与椭圆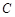 交于
交于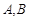 两点,且以
两点,且以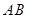 为直径的圆过椭圆右顶点
为直径的圆过椭圆右顶点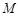 ,求证:直线l恒过定点.
,求证:直线l恒过定点.
如图,两座建筑物AB,CD的底部都在同一个水平面上,且均与水平面垂直,它们的高度分别是9m和15m,从建筑物AB的顶部A看建筑物CD的张角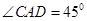 .
.
(1)求BC的长度;
(2)在线段BC上取一点P(点P与点B,C不重合),从点P看这两座建筑物的张角分别为 ,
,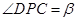 ,问点P在何处时,
,问点P在何处时, 最小?
最小?