如图，在四棱锥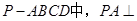
平面ABCD，
，E为PD的中点，F在AD上且
．
（1）求证：CE//平面PAB；
（2）若PA=2AB=2，求四面体PACE的体积．
在非负数构成的
数表
中每行的数互不相同，前6列中每列的三数之和为1，
，
，
，
，
，
，
均大于．如果
的前三列构成的数表
满足下面的性质
：对于数表中的任意一列
（
，2，…，9）均存在某个
使得
⑶
．
求证：
（ⅰ）最小值
，
，2，3一定自数表
的不同列．
（ⅱ）存在数表中唯一的一列
，
，2，3使得
数表
仍然具有性质．
设
，
是给定的两个正整数．证明：有无穷多个正整数
，使得
与互素．
求证不等式：
，
，2，…
如图，
，
分别为锐角三角形
（
）的外接圆
上弧
、
的中点．过点
作
交圆于
点，
为的内心，连接
并延长交圆于
．
⑴求证：
；
⑵在弧
（不含点）上任取一点
（
，，
），记
，
的内心分别为
，
，
求证：，，，四点共圆．
（本小题满分15分）求函数
的最大和最小值．