根据如图所示的程序框图，将输出的x、y值依次分别记为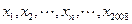
；
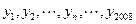
（Ⅰ）求数列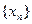
的通项公式
；
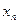（Ⅱ）写出y1，y2，y3，y4，由此猜想出数列{yn}的一个通项公式yn，并证明你的结论；
（Ⅲ）求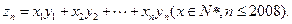
已知集合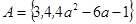
，
，
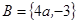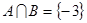，求实数
的值及此时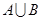
.
已知二次函数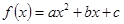
（其中
）满足下列3个条件：
①
的图象过坐标原点；
②对于任意
都有
成立；
③方程
有两个相等的实数根，令
（其中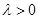
），
（1）求函数的表达式；
（2）求函数
的单调区间（直接写出结果即可）；
（3）研究函数在区间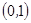
上的零点个数.
已知函数
，
（1）判断
的奇偶性并说明理由；
（2）当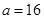
时，判断在
上的单调性并用定义证明；
（3）当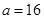时，若对任意
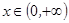，不等式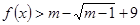
恒成立，求实数
的取值范围.
某商场经调查得知，一种商品的月销售量
（单位：吨）与销售价格（单位：万元/吨）的关系可用下图的一条折线表示．
（1）写出月销售量关于销售价格的函数关系式；
（2）如果该商品的进价为
万元/吨，除去进货成本外，商场销售该商品每月的固定成本为
万元，问该商品每吨定价多少万元时，销售该商品的月利润最大？并求月利润的最大值．
已知函数
（其中
且
）
（1）判断函数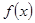
的奇偶性并证明；
（2）解不等式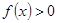
.