(本小题满分14分)已知函数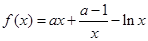 .
.
(1)若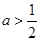 ,讨论函数的单调性;
,讨论函数的单调性;
(2)若方程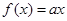 有两个相异实根,求实数
有两个相异实根,求实数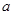 的取值范围.
的取值范围.
(本小题满分13分)已知椭圆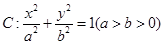 ,过焦点垂直于长轴的弦长为1,且焦点与短轴两端点构成等边三角形.
,过焦点垂直于长轴的弦长为1,且焦点与短轴两端点构成等边三角形.
(1)求椭圆的方程;
(2)过点Q(-1,0)的直线l交椭圆于A,B两点,交直线x=-4于点E,若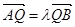 ,
,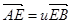 ,求证λ+μ为定值,并计算出该定值.
,求证λ+μ为定值,并计算出该定值.
(本小题满分12分)已知等差数列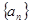 满足:
满足: ,
, ,该数列的前三项分别加上
,该数列的前三项分别加上 后顺次成为等比数列
后顺次成为等比数列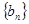 的前三项
的前三项
(1)分别求数列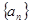 ,
,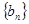 的通项公式
的通项公式 ,
, ;
;
(2)设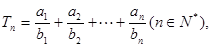 若
若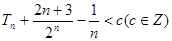 恒成立,求
恒成立,求 的最小值.
的最小值.
(本小题满分12分)如图,三角形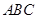 中,
中,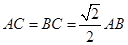 ,
, 是边长为
是边长为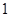 的正方形,平面
的正方形,平面 ⊥平面
⊥平面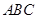 ,若
,若 分别是
分别是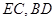 的中点.
的中点.
(1)求证: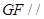 平面
平面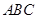 ;
;
(2)求证: ⊥平面
⊥平面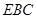 ;
;
(3)求几何体 的体积.
的体积.
(本小题满分12分)甲乙两人用四张扑克牌(红桃2,红桃3,红桃4,方片4)玩游戏,将牌洗匀后,背面朝上,按如下规则抽取:甲先抽,乙后抽,抽取的牌不放回,各抽取一张。
写出甲乙两人抽到牌的所有情况;
若甲抽到红桃3,则乙抽出的牌的牌面数字比3大的概率是多少?
甲乙约定:若甲抽出的牌的牌面数字比乙大,则甲胜;反之,则乙胜.你认为此游戏是否公平?说明你的理由.