（本小题满分12分）
某大学
毕业生参加一个公司的招聘考试，考试分笔试和面试两个环节，笔试有A、B两个题目，该学生答对A、B两题的概率分别为
、
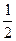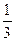，两题全部答对方可进入面试．面试要回答甲、乙两个问题，该学生答对这两个问题的概率均为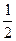，至少答对一题即可被聘用（假
设每个环节的每个问题回答正确与否是相互独立的）．
（I）求该学生被公司聘用的概率；
（II）设该学生答对题目的个数为
，求的分布列和数学
期望．
如图，已知长方体ABCD－A1B1C1D1中，AB＝3，BC＝2，CC1＝5，E是棱CC1上不同于端点的点，且
．
（1） 当∠BEA1为钝角时，求实数λ的取值范围；
（2） 若λ＝
，记二面角B1－A1B－E的的大小为θ，求|cosθ|．
已知a，b是正数，且a＋b＝1，求证：(ax＋by)(bx＋ay)≥xy．
在平面直角坐标系xOy中，已知直线l的参数方程为
(t为参数 )，圆C的参数方程为
(θ为参数)．若点P是圆C上的动点，求点P到直线l的距离的最小值．
已知矩阵A＝
属于特征值l的一个特征向量为α＝
．
（1）求实数b，l的值；
（2）若曲线C在矩阵A对应的变换作用下，得到的曲线为C¢：x2＋2y2＝2，求曲线C的方程．
如图，PA是圆O的切线，A为切点，PO与圆O交于点B、C，AQ^OP，垂足为Q．若PA＝4，PC＝2，求AQ的长．