(本小题满分12分)
为了研究某高校大学新生学生的视力情况,随机地抽查了该校100名进校学生的视力情况,得到频率分布直方图,如图.已知前4组的频数从左到右依次是等比数列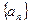 的前四项,后6组的频数从左到右依次是等差数列
的前四项,后6组的频数从左到右依次是等差数列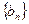 的前六项.
的前六项.
(I)求等比数列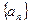 的通项公式;
的通项公式;
(II)求等差数列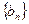 的通项公式;
的通项公式;
(III)若规定视力低于5.0的学生属于近视学生,试估计该校新生的近视率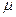 的大小.
的大小.
(本小题满分10分)
有两颗正四面体的玩具,其四个面上分别标有数字1,2,3,4,下面做投掷这两颗正四面体玩具的试验:用 表示结果,其中
表示结果,其中 表示投掷第1颗正四面体玩具落在底面的数字,
表示投掷第1颗正四面体玩具落在底面的数字, 表示投掷第2颗正四面体玩具落在底面的数字。
表示投掷第2颗正四面体玩具落在底面的数字。
(1)写出试验的基本事件;
(2)求事件“落在底面的数字之和大于3”的概率;
(3)求事件“落在底面的数字相等”的概率。
(本小题满分12分)
已知函数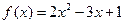 ,
, ,(
,(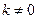 )
)
(1)问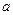 取何值时,方程
取何值时,方程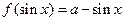 在
在 上有两解;
上有两解;
(2)若对任意的 ,总存在
,总存在 ,使
,使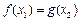 成立,求实数
成立,求实数 的取值范围?
的取值范围?
(本小题满分10分)
已知等差数列 的前四项和为10,且
的前四项和为10,且 成等比数列。
成等比数列。
(1)求通项公式 ;(2)设
;(2)设 ,求数列
,求数列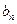 的前
的前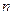 项和
项和
(本小题满分10分)如图,在三棱锥 中,三条棱
中,三条棱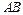 、
、 、
、 两两垂直,且
两两垂直,且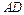 与平面
与平面 成
成 角,与平面
角,与平面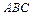 成
成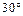 角.
角.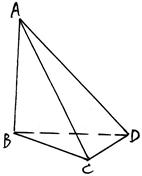
(1)由该棱锥相邻的两个面组成的二面角中,指出所有的直二面角;
(2)求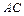 与平面
与平面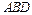 所成角的大小;
所成角的大小;
(3)求二面角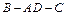 大小的余弦值.
大小的余弦值.
(本小题满分10分)△ABC中, 是A,B,C所对的边,S是该三角形的面积,且
是A,B,C所对的边,S是该三角形的面积,且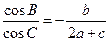 。
。
(1)求∠B的大小;
(2)若 =4,
=4, ,求
,求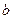 的值。
的值。