已知焦点在x轴上的双曲线C的两条渐近线经过坐标原点,并且两条渐近线与以点 为圆心、1为半径的圆相切,双曲线C的一个焦点与点A关于直线
为圆心、1为半径的圆相切,双曲线C的一个焦点与点A关于直线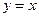 对称. (1)求双曲线C的渐近线和双曲线的方程;(2)设直线
对称. (1)求双曲线C的渐近线和双曲线的方程;(2)设直线 与双曲线C的左支交于P、Q两点,另一直线
与双曲线C的左支交于P、Q两点,另一直线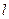 经过
经过 及线段PQ的中点N,求直线
及线段PQ的中点N,求直线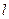 在
在 轴的截距
轴的截距 的取值范围.
的取值范围.
旅游公司为4个旅游团提供5条旅游线路,每个旅游团任选其中一条.
(1)求4个旅游团选择互不相同的线路共有多少种方法;
(2)求恰有2条线路被选中的概率;
(3)求选择甲线路旅游团数的数学期望.
如图:直三棱柱(侧棱⊥底面)ABC—A1B1C1中,∠ACB=90°,AA1=AC=1,BC= ,CD⊥AB,垂足为D.
,CD⊥AB,垂足为D.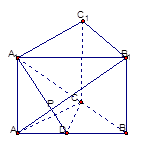
(1)求证:BC∥平面AB1C1;
(2)求点B1到面A1CD的距离.
如图,两个圆形飞轮通过皮带传动,大飞轮O1的半径为2r(r为常数),小飞轮O2的半径为r,O1O2=4r.在大飞轮的边缘上有两个点A,B,满足∠BO1A=,在小飞轮的边缘上有点C.设大飞轮逆时针旋转,传动开始时,点B,C在水平直线O1O2上.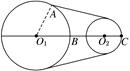
(1)求点A到达最高点时A,C间的距离;
(2)求点B,C在传动过程中高度差的最大值.
春节前,有超过20万名广西,四川等省籍的外来务工人员选择驾乘摩托车沿321国道长途跋涉返乡过年,为防止摩托车驾驶人员因长途疲劳驾驶,手脚僵硬影响驾驶操作而引发交通事故,肇庆市公安交警部门在321国道沿线设立了多个长途行驶摩托车驾驶人员休息站,让过往返乡过年的摩托车驾驶人员有一个停车休息的场所.交警小李在某休息站连续5天对进站休息的驾驶人员每隔50辆摩托车就进行省籍询问一次,询问结果如图所示.
(1)问交警小李对进站休息的驾驶人员的省籍询问采用的是什么抽样方法;
(2)用分层抽样的方法对被询问了省籍的驾驶人员进行抽样,若广西籍的被抽取了5名,则四川籍的应抽取几名?
(3)在上述抽出的驾驶人员中任取2名,求至少有1名驾驶人员是广西籍的概率.
设数列{an}的各项均为正数.若对任意的n∈N*,存在k∈N*,使得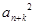 =an·an+2k成立,则称数列{an}为“Jk型”数列.
=an·an+2k成立,则称数列{an}为“Jk型”数列.
(1)若数列{an}是“J2型”数列,且a2=8,a8=1,求a2n;
(2)若数列{an}既是“J3型”数列,又是“J4型”数列,证明:数列{an}是等比数列.