设数列{an}的各项均为正数.若对任意的n∈N*,存在k∈N*,使得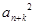 =an·an+2k成立,则称数列{an}为“Jk型”数列.
=an·an+2k成立,则称数列{an}为“Jk型”数列.
(1)若数列{an}是“J2型”数列,且a2=8,a8=1,求a2n;
(2)若数列{an}既是“J3型”数列,又是“J4型”数列,证明:数列{an}是等比数列.
(本小题满分12分)
已知函数 (其中常数
(其中常数 ).
).
(1)求函数 的定义域及单调区间;
的定义域及单调区间;
(2)若存在实数 ,使得不等式
,使得不等式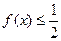 成立,求
成立,求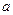 的取值范围。
的取值范围。
(本小题满分13分)
已知函数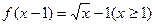 ,函数
,函数 的反函数为
的反函数为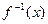 。
。
(1)求函数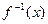 的解析式及定义域;
的解析式及定义域;
(2)若函数 在
在 上的最小值为3,求实数
上的最小值为3,求实数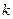 的值。
的值。
(本小题满分13分)
已知函数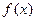 =
= 为偶函数,且函数
为偶函数,且函数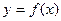 的图象的两相邻对称轴间的距离为
的图象的两相邻对称轴间的距离为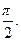
(Ⅰ)求f( )的值;
)的值;
(Ⅱ)将函数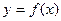 的图象向右平移
的图象向右平移 个单位后,再将得到的图象上各点的横坐标伸长到原来的4倍,纵坐标不变,得到函数
个单位后,再将得到的图象上各点的横坐标伸长到原来的4倍,纵坐标不变,得到函数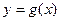 的图象,求
的图象,求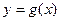 的单调递减区间.
的单调递减区间.
(本小题满分13分)
已知已知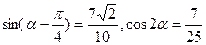 .
.
(1)求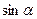 、
、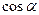 ;
;
(2)求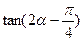 .
.
已知函数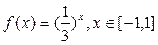 ,函数
,函数
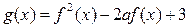 的最小值为
的最小值为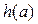 。
。
(1)求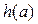 的表达式。
的表达式。
(2)是否存在实数m,n同时满足以下条件:
① m>n>3;
② 当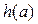 的定义域为[m,n]时,值域为
的定义域为[m,n]时,值域为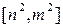
若存在,求出m,n的值;若不存在,说明理由。