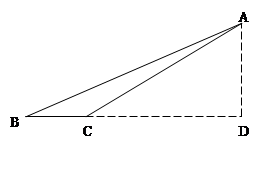已知 ,设命题
,设命题 :不等式
:不等式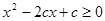 解集为R;命题
解集为R;命题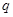 :方程
:方程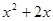
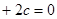 没有实根,如果命题p或q为真命题,p且q为假命题,求
没有实根,如果命题p或q为真命题,p且q为假命题,求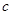 的取值范围.
的取值范围.
已知数列 的首项
的首项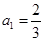 ,
, ,
,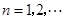 .
.
(Ⅰ)求证:数列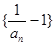 是等比数列;
是等比数列;
(Ⅱ)求数列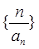 的前
的前 项和
项和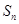 .
.
已知 是等比数列,
是等比数列, 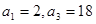 ,
,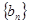 是等差数列,
是等差数列,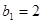
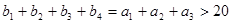
(1)求数列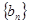 的通项公式;
的通项公式;
(2)求数列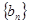 的前n项和
的前n项和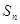 ;
;
(3)设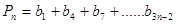 ,
, 其中n=1,2,......,试比较
其中n=1,2,......,试比较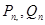 的大小。
的大小。
某家具厂有方木料90m3,五合板600m2,准备加工成书桌和书橱出售.已知生产每张书桌需要方木料0.1m3,五合板2m2,生产每个书橱需要方木料0.2m2,五合板1m2,出售一张方桌可获利润80元,出售一个书橱可获利润120元.怎样安排生产可使所得利润最大?最大利润为多少?
在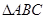 中,
中,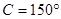 ,
, ,
,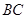 边的高设为
边的高设为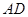 ,且
,且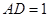 ,根据上述条件求:
,根据上述条件求:
(1) 的值;
的值;
(2)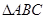 的面积.
的面积.