(本小题满分12分)通过研究学生的学习行为,心理学家发现,学生接受能力依赖于老师引入概念和描述问题所用的时间,讲座开始时,学生的兴趣激增,中间有一段不太长的时间,学生的兴趣保持理想的状态,随后学生的注意力开始分散.分析结果和实验表明,用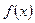 表示学生掌握和接受概念的能力(
表示学生掌握和接受概念的能力(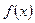 的值越大,表示接受能力越强),
的值越大,表示接受能力越强), 表示提出和讲授概念的时间(单位:分),可以有以下公式:
表示提出和讲授概念的时间(单位:分),可以有以下公式: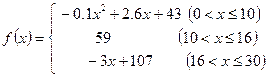
(1)开讲多少分钟后,学生的接受能力最强?能维持多少分钟?
(2)开讲 分钟与开讲
分钟与开讲 分钟比较,学生的接受能力何时强一些?
分钟比较,学生的接受能力何时强一些?
(3)一个数学难题,需要 的接受能力以及
的接受能力以及 分钟的时间,老师能否及时在学生一直达到所需接受能力的状态下讲授完这个难题?
分钟的时间,老师能否及时在学生一直达到所需接受能力的状态下讲授完这个难题?
(本小题满分14分) 若椭圆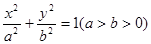 过点
过点 ,离心率为
,离心率为 ,⊙O的圆心在原点,直径为椭圆的短轴,⊙M的方程为
,⊙O的圆心在原点,直径为椭圆的短轴,⊙M的方程为 ,过⊙M上任一点P作⊙O的切线PA、PB,切点为A、B.
,过⊙M上任一点P作⊙O的切线PA、PB,切点为A、B.
(1) 求椭圆的方程;
(2)若直线PA与⊙M的另一交点为Q,当弦PQ最大时,求直线PA的方程。
(本小题满分14分)已知:三次函数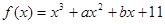 ,在
,在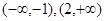 上单调递增,在
上单调递增,在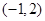 上单调递减
上单调递减
(1)求函数f (x)的解析式;
|
(2)求函数f (x)在区间[-2,2]的最值。
(本小题满分14分)
如图所示的长方体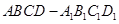 中,底面
中,底面 是边长为
是边长为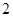 的正方形,
的正方形, 为
为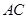 与
与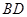 的交点,
的交点,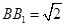 ,
,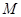 是线段
是线段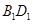 的中点.
的中点.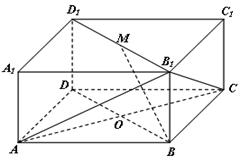
(1)求证: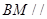 平面
平面 ;
;
(2)求三棱锥D1-ABC的体积.
(本小题满分14分)
通过随机询问某校110名高中学生在购买食物时是否看营养说明,得到如下的列联表: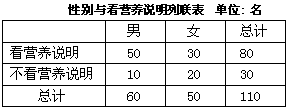
(1)从这50名女生中按是否看营养说明采取分层抽样,抽取一个容量为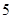 的样本,问样本中看与不看营养说明的女生各有多少名?
的样本,问样本中看与不看营养说明的女生各有多少名?
(2) 从(1)中的5名女生样本中随机选取两名作深度访谈, 求选到看与不看营养说明的女生各一名的概率;
(3)根据以上列联表,问有多大把握认为“性别与在购买食物时看营养说明”有关?
(本小题满分12分)
已知数列 是一个等差数列,且
是一个等差数列,且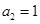 ,
,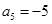 .(1)求
.(1)求 的通项
的通项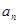 ;
;
(2) 求 前
前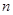 项和
项和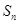 ;
;