(本小题满分13分)
已知 ,
, ,f(x)=
,f(x)=

⑴ 求f(x)的最小正周期和单调增区间;
⑵ 如果三角形ABC中,满足f(A)= ,求角A的值.
,求角A的值.
如图,AB、CD均为圆O的直径,CE⊥圆O所在的平面,BF∥CE.求证: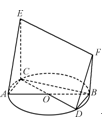
(1)平面BCEF⊥平面ACE;
(2)直线DF∥平面ACE.
如图,在正三棱柱ABCDEF中,AB=2,AD=1.P是CF的延长线上一点,FP=t.过A、B、P三点的平面交FD于M,交FE于N.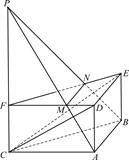
(1)求证:MN∥平面CDE;
(2)当平面PAB⊥平面CDE时,求t的值.
如图,正方形ABCD和三角形ACE所在的平面互相垂直.EF∥BD,AB= EF.求证:
EF.求证:
(1)BF∥平面ACE;
(2)BF⊥BD.
在如图所示的多面体中,已知正三棱柱ABCA1B1C1的所有棱长均为2,四边形ABDC是菱形.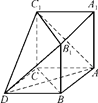
(1)求证:平面ADC1⊥平面BCC1B1;
(2)求该多面体的体积.
如图,在直四棱柱ABCDA1B1C1D1中,底面ABCD为等腰梯形,AB∥CD,且AB=2CD,在棱AB上是否存在一点F,使平面C1CF∥平面ADD1A1?若存在,求点F的位置;若不存在,请说明理由.