某高级中学共有学生2000名,各年级男、女生人数如下表:
| |
高一年级 |
高二年级 |
高三年级 |
| 女生 |
373 |
x |
y |
| 男生 |
377 |
370 |
z |
已知在全校学生中随机抽取1名,抽到高二年级女生的概率是0.19.
(Ⅰ)求x的值;
(Ⅱ)现 用分层抽样的方法在全校抽取48名学生,问应在高三年级抽取多少名?
用分层抽样的方法在全校抽取48名学生,问应在高三年级抽取多少名?
如右图所示,在三棱锥A-BCD中,E,F,G,H分别是边AB,BC,CD,DA的中点.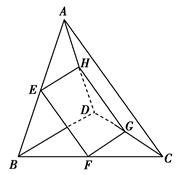
(1)求证:四边形EFGH是平行四边形;
(2)若AC=BD,求证:四边形EFGH是菱形;
(3)当AC与BD满足什么条件时,四边形EFGH是正方形
如右图所示,在四棱锥P—ABCD中,底面ABCD是矩形,PA⊥底面ABCD,PA=AB=1,AD=,点F是PB的中点,点E在边BC上移动.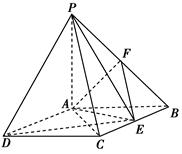
(1)求三棱锥E—PAD的体积;
(2)当点E为BC的中点时,试判断EF与平面PAC的位置关系,并说明理由;
(3)证明:无论点E在边BC的何处,都有PE⊥AF.
如右图所示,ABCD-A1B1C1D1是正四棱柱,侧棱长为1,底面边长为2,E是棱BC的中点.
(1)求证:BD1∥平面C1DE;
(2)求三棱锥D-D1BC的体积
一几何体的表面展开图如右图,则这个几何体是哪一种几何体?选择适当的角度,画出它水平放置时的直观图与三视图.并计算该几何体的体积.
如右图所示,在正三棱柱ABC—A1B1C1中,AB=3,AA1=4,M为AA1的中点,P是BC上一点,且由P沿棱柱侧面经过棱CC1到M的最短路线长为,设这条最短路线与CC1的交点为N.求: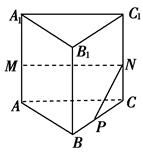
(1)该三棱柱的侧面展开图的对角线长;
(2)PC和NC的长.