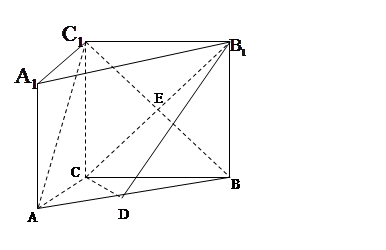设命题p:函数 在R上单调递增,命题q:不等式
在R上单调递增,命题q:不等式
对于 恒成立,若“
恒成立,若“ ”为假,“
”为假,“ ”为真,求实数
”为真,求实数 的取值范围
的取值范围
为了某班学生喜爱打篮球是否与性别有关,对本班50人进行问卷调查得到了如下的列联表:
已知在全部50人中随机抽取1人,抽到不爱打篮球的学生的概率为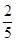 .
.
(1)请将上面的列联表补充完整;
(2)是否有把握在犯错误的概率不超过0.005的前提下认为喜爱打篮球与性别有关;请说明理由.
附参考公式:
P( ) ) |
0.05 |
0.025 |
0.010 |
0.005 |
0.001 |
| k |
3.841 |
5.024 |
6.635 |
7.879 |
10.828 |
已知A={x||x-a|<4},B={x| }.
}.
(1)若a=1,求 ;
;
(2)若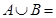 R,求实数a的取值范围.
R,求实数a的取值范围.
列三角形数表
假设第 行的第二个数为
行的第二个数为
(1)依次写出第六行的所有数字;
(2)归纳出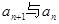 的关系式并求出
的关系式并求出 的通项公式;
的通项公式;
(3)设 求证:
求证: …
…
如图,在直三棱柱ABC--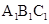 中,AC=3,BC=4,AB=5,
中,AC=3,BC=4,AB=5, ,点D是AB的中点。
,点D是AB的中点。
(1)求证: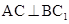 ;
;
(2)求证: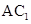 ∥平面
∥平面