(本小题14分)已知函数 在
在 处取得极值。
处取得极值。
(Ⅰ)求函数 的解析式;
的解析式;
(Ⅱ)求证:对于区间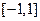 上任意两个自变量的值
上任意两个自变量的值 ,都有
,都有 ;
;
(Ⅲ)若过点 可作曲线
可作曲线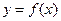 的三条切线,求实数
的三条切线,求实数 的取值范围。
的取值范围。
如图,已知正方体ABCD-A1B1C1D1中,M是AA1的中点,N是BB1的中点.求证:平面MDB1∥平面ANC.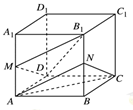
已知函数 是
是 上的偶函数,其图象关于点
上的偶函数,其图象关于点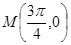 对称,且在区间
对称,且在区间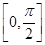 上是单调函数,求
上是单调函数,求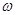 和
和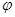 的值.
的值.
向量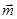 =
=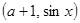 ,
,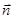 =
=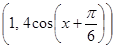 ,设函数
,设函数 =
=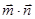 (a∈
(a∈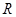 ,且a为常数).
,且a为常数).
(1)若 为任意实数,求
为任意实数,求 的最小正周期;
的最小正周期;
(2)若 在
在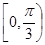 上的最大值与最小值之和为7,求
上的最大值与最小值之和为7,求 的值.
的值.
为积极配合湛江市2015年省运会志愿者招募工作,某大学数学学院拟成立由4名同学组成的志愿者招募宣传队,经过初步选定,2名男同学,4名女同学共6名同学成为候选人,每位候选人当选宣传队队员的机会是相同的.
(1)求当选的4名同学中恰有1名男同学的概率;
(2)求当选的4名同学中至少有3名女同学的概率.
已知 ,
,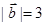 ,
,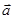 与
与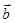 的夹角为
的夹角为 .
.
求(1) ;(2)
;(2) .
.