已知函数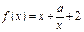 (
(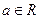 )
)
(1)若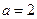 ,求
,求 在
在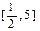 上的最小值和最大值;
上的最小值和最大值;
(2)如果 对
对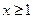 恒成立,求实数
恒成立,求实数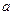 的取值范围
的取值范围
某种牌号的汽车在水泥路面上的刹车距离 m和汽车车速
m和汽车车速 km/h有如下关系:
km/h有如下关系: .
.
在这次交通事故中,测得这种车的刹车距离大于39.5 m,那么这辆汽车刹车前的车速至少为多少?(精确到0.01 km/h)
已知函数 ,求使函数值大于
,求使函数值大于 的
的 的取值范围
的取值范围
某单位建造一间背面靠墙的小房,地面面积为12 m ,房屋正面每平方米的造价为
,房屋正面每平方米的造价为 元,房屋侧面每平方米的造价为
元,房屋侧面每平方米的造价为 元,屋顶的造价为
元,屋顶的造价为 元.如果墙高为
元.如果墙高为 m,且不计房屋背面和地面的费用,问怎样设计房屋能使总等价最低?最低总造价是多少?
m,且不计房屋背面和地面的费用,问怎样设计房屋能使总等价最低?最低总造价是多少?
若关于 的一元二次方程
的一元二次方程 有两个不相等的实数根,求
有两个不相等的实数根,求 的取值范围.
的取值范围.
有一个两位数大于50而小于60,其个位数字比十位数字大2.试用不等式表示上述关系,并求出这个两位数(用 和
和 分别表示这个两位数的十位数字和个位数字).
分别表示这个两位数的十位数字和个位数字).