(本小题满分12分)高二级某次数学测试中,随机从该年级所有学生中抽取了100名同学的数学成绩(满分150分),经统计成绩在
的有6人,在
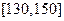的有4人.在
,
各区间分布情况如右图所示的频率分布直方图,若直方图中,
和
对应小矩形高度相等,且
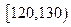对应小矩形高度又恰为对应小矩形高度的一半.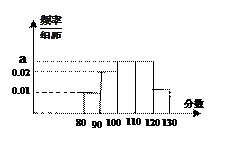
(1)确定图中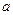
的值;
(2)设得分在110分以上(含110分)为优秀,则这次测试的优秀率是多少?
(3)某班共有学生50人,若以该次统计结果为依据,现随机从该班学生中抽出3人, 则至少抽到一名数学成绩优秀学生的概率是多少?
（本小题满分12分）四棱锥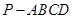
的底面是正方形，
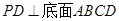，点E在棱PB上.若AB=
,
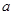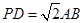
（Ⅰ）求证：平面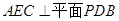
；
（Ⅱ）若E为PB的中点时，求AE与平面PDB所成的角的大小.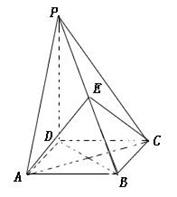
某校从参加高二年级期中考试的学生中抽出60名学生，将其成绩（均为整数）分成六段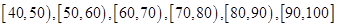
后，画出如下部分频率分布直方图。观察图形，回答下列问题：
（1）求第四小组的频率，并补全这个频率分布直方图;
（2）估计这次考试的及格率（60分以上为及格）;
（3）估计这次考试的平均分。
（本小题满分12分）
有4张面值相同的债券，其中有2张中奖债券.
（1）有放回地从债券中任取2次，每次取出1张，计算取出的2张都是中奖债券的概率.
（2）无放回地从债券中任取2次，每次取出1张，计算取出的2张中至少有1张是中奖债券的概率.
（本小题满分14分）（注意：仙中、一中、八中的学生三问全做，其他学校的学生只做前两问）
已知函数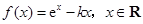
（Ⅰ）若
，试确定函数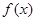
的单调区间；
（Ⅱ）若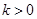
，且对于任意
，
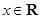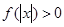恒成立，试确定实数
的取值范围；
（Ⅲ）设函数
，求证：
．
（本小题满分13分）
已知数列{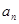
}满足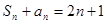
,
（I）写出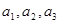
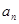,并推测的表达式；
（II）用数学归纳法证明所得的结论。