(本小题12分)已知F1,F2是椭圆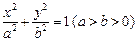 的左、右焦点,点P(-1,
的左、右焦点,点P(-1,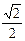 )在椭圆上,线段PF2与
)在椭圆上,线段PF2与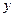 轴的交点
轴的交点 满足
满足 .(1)求椭圆的标准方程;
.(1)求椭圆的标准方程;
(2)过F1作不与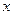 轴重合的直线
轴重合的直线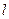 ,
,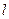 与圆
与圆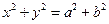 相交于A、B.并与椭圆相交于C、D.当
相交于A、B.并与椭圆相交于C、D.当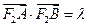 ,且
,且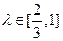 时,求△F2CD的面积S的取值范围.
时,求△F2CD的面积S的取值范围.
(本小题12分)
已知函数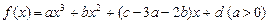 的图像如图所示.
的图像如图所示.
(1)求 的值;
的值;
(2)若函数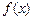 在
在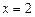 处的切线方程为
处的切线方程为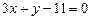 ,
,
求函数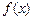 的解析式;
的解析式;
(3)若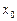 =5,方程
=5,方程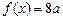 有三个不同的根,求实数
有三个不同的根,求实数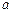 的取值范围。
的取值范围。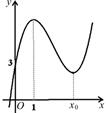
(本小题12分)如图,四棱锥 中,
中,
侧面 是边长为2的正三角形,且与底面垂直,底面
是边长为2的正三角形,且与底面垂直,底面 是
是 的菱形,
的菱形,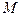 为
为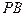 的中点.
的中点.
(1)求 与底面
与底面 所成角的大小;
所成角的大小;
(2)求证: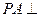 平面
平面 ;
;
(3)求二面角 的余弦值.
的余弦值. 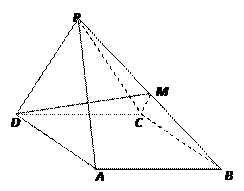
已知各项均为正数的数列 满足
满足 其中n=1,2,3,….(1)求
其中n=1,2,3,….(1)求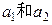 的值;(2)求证:
的值;(2)求证: ;
;
(本小题12分)某公司在过去几年内使用某种型号的灯管1000支,该公司对这些灯管的使用寿命(单位:小时)进行了统计,统计结果如下表所示:
| 分组 |
[500,900) |
[900,1100) |
[1100,1300) |
[1300,1500) |
[1500,1700) |
[1700,1900) |
[1900, ) ) |
| 频数 |
48 |
121 |
208 |
223 |
193 |
165 |
42 |
| 频率 |
(1)将各组的频率填入表中;
(2)根据上述统计结果,计算灯管使用寿命不足1500小时的频率;
(3)该公司某办公室新安装了这种型号的灯管3支,若将上述频率作为概率,试求至少有2支灯管的使用寿命不足1500小时的概率.