（本小题满分13分）已
知
是函数
的极值点．
（1）当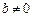
时，讨论函数
的单调性；
（2）当
R时，函数
有两个零点，求实数m的取值范围.
（本小题满分13分）从装有2只红球，2只白球和1只黑球的袋中逐一取球，已知每只球被抽取的可能性相同。
（1）若抽取后又放回，抽3次，①分别求恰2次为红球的概率及抽全三种颜色球的概率；②求抽到红球次数
的数学期望.
（2）若抽取后不放回，抽完红球所需次数为
的分布列及期望.
交通指数是交通拥堵指数的简称，是综合反映道路网畅通或拥堵的概念，记交通指数为
．其范围为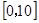
，分别有五个级别：
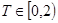畅通;
基本畅通;
轻度拥堵;
中度拥堵；
严重拥堵．在晚高峰时段(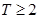
)，从某市交通指挥中心选取了市区20个交通路段，依据其交通指数数据绘制的频率分布直方图如图所示．
(1)在这20个路段中，轻度拥堵、中度拥堵的路段各有多少个？
(2)从这20个路段中随机抽出3个路段，用X表示抽取的中度拥堵的路段的个数，求X的分布列及期望．
已知(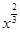
＋3x2)n的展开式中，各项系数和比它的二项式系数和大992，求：
(1)展开式中二项式系数最大的项；
(2)展开式中系数最大的项．
已知不等式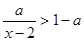
（1）若
，求关于
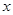不等式的解集；（2）若
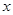，求关于不等式的解集.
数列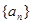
满足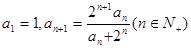
（1）证明:数列
是等差数列；（2）求数列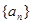的通项公式
；
（3）设
，求数列
的前
项和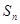
.