（本小题满分12分）
某产品生产厂家根据以往的生产销售经验得到下面有关销售的统计规律：每生产产品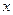
（百台），其总成本为
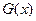万元，其中固定成本为2万元，并且每生产100台的生产成本为1万元（总成本=固定成本+生产成本），销售收入
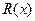满足
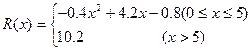。假定该产品销售平衡，
那么根据上述统计规律。
（1）要使工厂有盈利，产品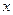应控制在什么范围？
（2）工厂生产多少台产品时赢利最大？并求此时每台产品的售价为多少？
（本小题12分）袋中有形状大小完全相同的8个小球，其中红球5个，白球3个。某人逐个从袋中取球，第一次取出一个小球，记下颜色后放回袋中；第二次取出一个小球，记下颜色后，不放回袋中，第三次取出一个小球，记下颜色后，放回袋中，第四次取出一个小球，记下颜色后不放回袋中……，如此进行下去，直到摸完球为止。
（1）求第四次恰好摸到红球的概率；
（2）记ξ为前三次摸到红球的个数，写出其分布列，并求其期望Eξ。
（本小题12分）四棱锥P-ABCD中，PA⊥底面ABCD，AB∥CD，AD=CD=1，∠BAD=120°，PA=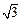
，∠ACB=90°。
（1）求证：BC⊥平面PAC；
（2）求二面角D-PC-A的大小的正切值；
（3）求点B到平面PCD的距离。
（本小题满分12分）已知数列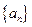
满足
（Ⅰ）求数列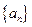的通项公式；
（Ⅱ）若数列
满足
，证明：
是等差数列；
（Ⅲ）证明：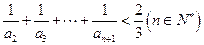
（本小题10分）已知向量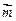
＝(1＋cosB，sinB)且与向量
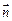=（0，1）所成的角为
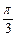，其中A、B、C为ΔABC的三个内角。
（1）求角B的大小；（2）若AC＝
，求ΔABC周长的最大值。
（本小题满分14分）椭圆E的中心在原点O，焦点在x轴上，离心率
，过点C（-1，0）的直线l交椭圆于A、B两点，且满足：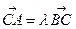
（λ≥2）。
（1）若λ为常数，试用直线l的斜率k（k≠0）表示三角形OAB的面积；
（2）若λ为常数，当三角形OAB的面积取得最大值时，求椭圆E的方程；
（3）若λ变化，且λ=k2+1，试问：实数λ和直线l的斜率k（k∈R）分别为何值时，椭圆E的短半轴长取得最大值？并求出此时的椭圆方程。