(本小题满分12分)已知函数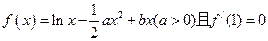 ,
,
(Ⅰ)试用含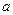 的式子表示b,并求函数
的式子表示b,并求函数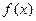 的单调区间;
的单调区间;
(Ⅱ)已知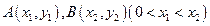 为函数
为函数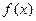 图象上不同两点,
图象上不同两点, 为
为 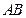 的中点,记AB两点连线斜率为K,证明:
的中点,记AB两点连线斜率为K,证明: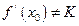
某高三学生的10科会考成绩中,有三科“优”,四科“良”,三科“及格”.从这10科成绩中任取3科,求①取出的三科成绩中“优”的料数X的分布列和数学期望;②取出的三科成绩中“优”多于“良”的概率
已知数列的前n项和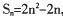 ,数列
,数列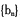 的前Ii项和
的前Ii项和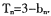 ①求数列
①求数列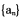 和
和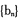 的
的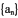 通项公式;②设
通项公式;②设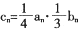 ,求数列
,求数列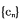 的前n项和
的前n项和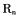 的表达式
的表达式
已知函数f(x)=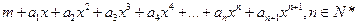 。
。
(I)若f(x)=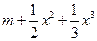 。
。
①求曲线y=f(x)上的点P(1,f(1))为切点的切线的斜率;
②若函数f(x)在x=x1处取得极大值,在x=x2处取得极小值,且点(x1,f(x1))在第二象限,点(x2,f(x2))位于y轴负半轴上,求m的取值范围;
(II)当an=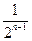 时,设函数f(x)的导函数为
时,设函数f(x)的导函数为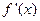 ,令Tn=
,令Tn=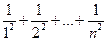 ,证明:Tn
,证明:Tn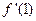 1
1
设数列{an}的首项为a1=1,前n项和为Sn,且Sn+1= 。
。
(I)求数列{an}的通项公式an;
(II)设数列{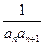 }的前n项和为Tn,是否存在最大正整数,使得对[1,+1]内的任意n
}的前n项和为Tn,是否存在最大正整数,使得对[1,+1]内的任意n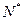 ,不等式n<
,不等式n< 恒成立?若存在,求出的值;若不存在,请说明理由。
恒成立?若存在,求出的值;若不存在,请说明理由。
已知函数f(x)=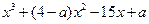 ,aR。
,aR。
(I)若点P(0,2)在函数f(x)的图象上,求a的值和函数f(x)的极小值;
(II)若函数f(x)在(1,1)上是单调递减函数,求a的最大值