(满分14分)为了在夏季降温和冬季供暖时减少能源损耗,房屋的屋顶和外墙需要建造隔热层。某幢建筑物要建造可使用20年的隔热层,每厘米厚的隔热层建造成本为6万元。该建筑物每年的能源消耗费用C(单位:万元)与隔热层厚度x(单位:cm)满足关系:C(x)=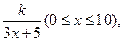 若不建隔热层,每年能源消耗费用为8万元。设
若不建隔热层,每年能源消耗费用为8万元。设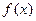 为隔热层建造费用
为隔热层建造费用 与20年的能源消耗费用之和。
与20年的能源消耗费用之和。
(1)求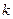 的值及
的值及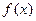 的表达式。
的表达式。
(2)隔热层修建多厚时,总费用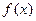 达到最小,并求最小值。
达到最小,并求最小值。
如图,在平面直角坐标系中,锐角 和钝角
和钝角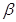 的终边分别与单位圆交于
的终边分别与单位圆交于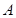 ,
, 两点.
两点.
(1)如果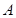 、
、 两点的纵坐标分别为
两点的纵坐标分别为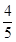 与
与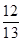 ,求
,求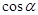 和
和 ;
;
(2)在⑴的条件下,求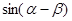 的值;
的值;
(3)已知点
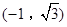 ,求函数
,求函数 的值域.
的值域.
某商品在近30天内每件的销售价格p(元)与时间t(天)的函数关系是 该商品的日销售量Q(件)与时间t(天)的函数关系是
该商品的日销售量Q(件)与时间t(天)的函数关系是
 ,求这种商品的日销售金额的最大值,并指出日销售金额最大的一天是30天中的第几天?
,求这种商品的日销售金额的最大值,并指出日销售金额最大的一天是30天中的第几天?
对于二次函数 ,
,
(1)指出图像的开口方向、对称轴方程、顶点坐标;
(2)画出它的图像,并说明其图像由 的图像经过怎样平移得来;
的图像经过怎样平移得来;
(3)求函数的最大值或最小值;
(4)分析函数的单调性。
证明:函数 是偶函数,且在
是偶函数,且在 上是增加的。
上是增加的。
设集合 ,集合
,集合 。
。
(1)当 为自然数集
为自然数集 时,求
时,求 的真子集的个数;
的真子集的个数;
(2)当 为实数集
为实数集 时,且
时,且 ,求
,求 的取值范围。。
的取值范围。。