（本小题满分14分）知圆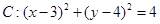
，直线
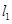过定点A（1，0）．
（1）若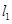与圆相切，求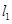的方程；
（2）若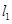与圆相交于P，Q两点，线段PQ的中点为M，又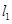与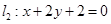
的交点为N，判断
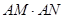是否为定值，若是，则求出定值；若不是，请说明理由。
已知函数：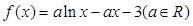
（I）讨论函数
的单调性；
（II）若函数
的图象在点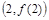
处的切线的倾斜角为45o，是否存在实数m使得对于任意的
，函数
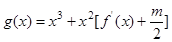在区间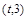
上总不是单调函数?若存在，求m的取值范围；否则，说明理由；
(Ⅲ)求证：
．
已知函数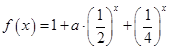
；
．
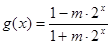(I)当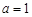
时，求函数f（x）在
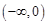上的值域；
（II）若对任意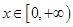
，总有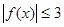
成立，求实数
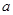的取值范围；
(Ⅲ)若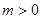
（
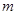为常数），且对任意
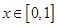，总有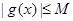
成立，求M的取值范围．
某企业在第1年初购买一台价值为120万元的设备M，M的价值在使用过程中逐年减少，从第2年到第6年，每年初M的价值比上年初减少10万元；从第7年开始，每年初M的价值为上年初的75%．
（I）求第n年初M的价值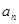
的表达式；
（II）设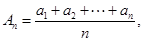
若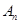
大于80万元，则M继续使用，否则须在第n年初对M更新，证明:必须在第9年初对M进行更新.
在△ABC中，角A的对边长等于2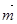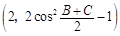，向量
=
，向量
=
.
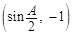(I)求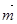·取得最大值时的角A的大小；
(II)在（1）的条件下，求△ABC面积的最大值.
成等差数列的三个正数的和等于15，并且这三个数分别加上2，5，13后成为等比数列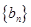
中的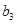
，
，
.
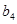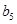(I) 求数列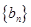的通项公式；
(II) 数列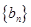的前n项和为
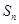，求证：数列
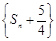是等比数列.