如图,椭圆的中心在原点, 为椭圆的左焦点,
为椭圆的左焦点, 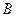 为椭圆的一个顶点,过点
为椭圆的一个顶点,过点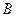 作与
作与 垂直的直线
垂直的直线 交
交 轴于
轴于 点, 且椭圆的长半轴长
点, 且椭圆的长半轴长 和短半轴长
和短半轴长 是关于
是关于 的方程
的方程 (其中
(其中 为半焦距)的两个根.
为半焦距)的两个根.
(1)求椭圆的离心率;
(2)经过 、
、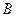 、
、 三点的圆与直线
三点的圆与直线 相切,试求椭圆的方程.
相切,试求椭圆的方程.
假设关于某种设备的使用年限 和支出的维修费用
和支出的维修费用 (万元),有以下的统计资料:
(万元),有以下的统计资料:
使用年限 |
2 |
3 |
4 |
5 |
6 |
维修费用 |
2.2 |
3.8 |
5.5 |
6.5 |
7.0 |
(1)求支出的维修费用 与使用年限
与使用年限 的线性回归方程;
的线性回归方程;
(2)估计使用年限为10年时,维修费用是多少?
( )
)
在直角坐标系xoy中,椭圆C1: 的左、右焦点分别为F1、F2,F2也是抛物线C2:
的左、右焦点分别为F1、F2,F2也是抛物线C2: 的焦点,点M为C1与C2在第一象限的交点,且
的焦点,点M为C1与C2在第一象限的交点,且 。
。
(1)求C1的方程;
(2)平面上的点N满足 ,直线
,直线 ∥MN,且与C1交于A、B两点,若
∥MN,且与C1交于A、B两点,若 ,求直线
,求直线 的方程。
的方程。
已知函数 在
在 处取得极值,且在点
处取得极值,且在点 处的切线的斜率为2。
处的切线的斜率为2。
(1)求a、b的值;
(2)求函数 的单调区间和极值;
的单调区间和极值;
(3)若关于x的方程 在
在 上恰有两个不相等的实数根,求实数m的取值范围。
上恰有两个不相等的实数根,求实数m的取值范围。
已知函数 ,当
,当 时,函数
时,函数 在x=2处取得最小值1。
在x=2处取得最小值1。
(1)求函数 的解析式;
的解析式;
(2)设k>0,解关于x的不等式 。
。
设 是定义在R上的奇函数,且对任意实数x,恒有
是定义在R上的奇函数,且对任意实数x,恒有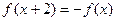 ,当
,当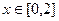 时,
时, 。
。
(1)求证: 是周期函数;
是周期函数;
(2)计算: 。
。