设集合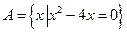 ,
,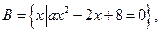
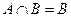 ,求
,求 的取值范围。
的取值范围。
.已知函数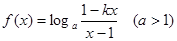 是奇函数
是奇函数
(1)求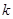 的值,并求出该函数的定义域;
的值,并求出该函数的定义域;
(2)根据(1)的结果,判断 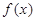 在
在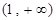 上的单调性,并给出证明.
上的单调性,并给出证明.
已知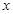
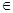 [
[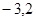 ],求函数
],求函数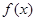 =
=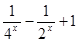 的最大值与最小值.
的最大值与最小值.
(本题满分10分) 选修4-5:不等式选讲
(Ⅰ)解关于x的不等式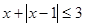 ;
;
(Ⅱ)若关于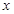 的不等式
的不等式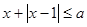 有解,求实数
有解,求实数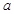 的取值范围.
的取值范围.
(本小题满分10分)选修4-4:坐标系与参数方程
已知曲线C的极坐标方程是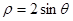 ,设直线
,设直线 的参数方程是
的参数方程是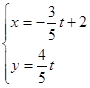 (
(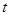 为参数)。
为参数)。
(Ⅰ)将曲线C的极坐标方程转化为直角坐标方程;
(Ⅱ)设直线 与
与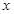 轴的交点是M,N为曲线C上一动点,求|MN|的最大值。
轴的交点是M,N为曲线C上一动点,求|MN|的最大值。
(本小题满分10分)选修4-1:几何证明选讲
如图,直线 经过⊙
经过⊙ 上的点
上的点 ,并且
,并且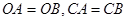 .⊙
.⊙ 交直线
交直线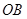 于
于 ,
, ,连接
,连接 .
.
(Ⅰ)求证:直线 是⊙
是⊙ 的切线;
的切线;
(Ⅱ)若 ,⊙
,⊙ 的半径为3,求
的半径为3,求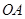 的长.
的长.