(本小题满分10分)选修4-4:坐标系与参数方程
已知曲线C的极坐标方程是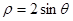 ,设直线
,设直线 的参数方程是
的参数方程是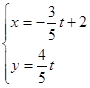 (
(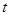 为参数)。
为参数)。
(Ⅰ)将曲线C的极坐标方程转化为直角坐标方程;
(Ⅱ)设直线 与
与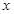 轴的交点是M,N为曲线C上一动点,求|MN|的最大值。
轴的交点是M,N为曲线C上一动点,求|MN|的最大值。
(已知双曲线的中心在原点,焦点F1、F2在坐标轴上,离心率为且过点(4,- )
)
(Ⅰ)求双曲线方程;
(Ⅱ)若点M(3,m)在双曲线上,求证:点M在以F1F2为直径的圆上;
(Ⅲ)求△F1MF2的面积.
已知点B(5,0)和点C(-5,0),过点B的直线l与过点C的直线m相交于点A,设直线l的斜率为k1,直线m的斜率为k2:
(Ⅰ)如果k1·k2=,求点A的轨迹方程;
(Ⅱ)如果k1·k2=a,其中a≠0,求点A的轨迹方程,并根据a的取值讨论此轨迹是何种曲线.
中心在原点,一焦点为F1(0,5 )的椭圆被直线y=3x-2截得的弦的中点横坐标是
)的椭圆被直线y=3x-2截得的弦的中点横坐标是 ,求此椭圆的方程。
,求此椭圆的方程。
椭圆的一个顶点为A(2,0),其长轴长是短轴长的2倍,求椭圆的标准方程.
求一条渐近线方程是 ,一个焦点是
,一个焦点是 的双曲线标准方程,并求此双曲线的离心率.
的双曲线标准方程,并求此双曲线的离心率.